 Intenzita gravitačného poľa, princíp superpozície
Intenzita gravitačného poľa, princíp superpozície
Popíšeme si teraz prípad, keď gravitačné pole je vytvorené hmotným bodom s hmotnosťou M. Do vzdialenosti r od neho položme „skúšobný“ hmotný bod s menšou hmotnosťou m ( jeho polohový vektor vzhľadom na prvý hmotný bod je r). Skúmajme gravitačné účinky bodu M na bod m. Vieme už, že príťažlivá sila je daná vzťahom
Pretože však v priestore okolo bodu M existuje gravitačné pole aj bez existencie bodu m, je výhodné zaviesť na charakterizovanie poľa takú veličinu, u ktorej hmotnosť m skúšobného hmotného bodu nie je obsiahnutá. Na tento účel je vhodná veličina intenzita gravitačného poľa K. Táto je definovaná ako podiel sily pôsobiacej na hmotný bod m, a hmotnosti tohto hmotného bodu, t.j.
Intenzita sa teda číselne rovná sile, pôsobiacej na hmotný bod o jednotkovej hmotnosti.
Z druhého Newtonovho zákona - zákona sily - vyplýva, že aj zrýchlenie je dané podielom sily a hmotnosti
takže
K = a (3.2.3.4)
Z toho vidíme, že intenzita v každom bode gravitačného poľa je totožná so zrýchlením, ktoré pole hmotnému bodu v tomto mieste udeľuje (za predpokladu, že tu nepôsobia ešte ďalšie sily). Na povrchu Zeme má hodnotu približne 9,81 N.m-1 (resp. 9,81 m.s –2 ; presná hodnota závisí od zemepisnej šírky).
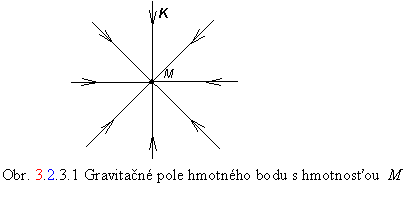
Gravitačné pole môžeme graficky znázorniť pomocou tzv. gravitačných siločiar. Sú to krivky, u ktorých dotyčnica v ľubovoľnom bode je totožná so smerom pôsobiacej gravitačnej sily, resp. so smerom vektora intenzity poľa. Gravitačné pole, vytvorené jedným hmotným bodom M, má radiálny charakter; gravitačné siločiary sú priestorovo symetricky rozložené polpriamky, prichádzajúce z nekonečna a vstupujúce do hmotného bodu, ktorý je zdrojom poľa (obr. 3.2.3.1 ).
Gravitačné pole, u ktorého má hodnota intenzity v každom mieste rovnakú hodnotu, nazývame homogénne. Za takéto môžeme považovať aj pole v relatívne malých výškach (rádovo desiatky, resp. stovky km) nad povrchom Zeme.
Princíp superpozície
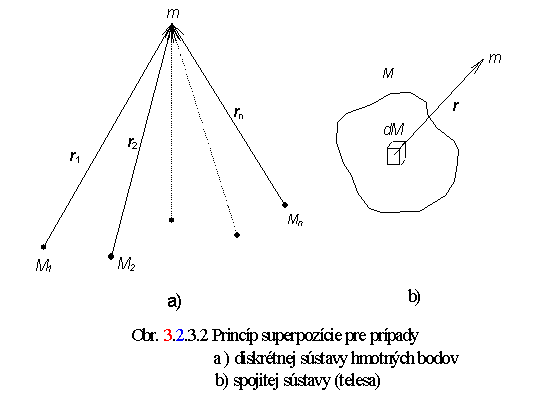
Predpokladajme, že gravitačné pole je vytvorené nie jedným, ale viacerými diskrétne rozloženými hmotnými bodmi s hmotnosťami M1, M2,... Mn. Každý z nich je takto zdrojom vlastného gravitačného poľa. Nech polohové vektory skúšobného hmotného bodu s hmotnosťami m vzhľadom na body, vytvárajú pole, sú r1, r2,..., rn (obr. 3.2.3.2a). Výsledné gravitačné pôsobenie na skúšobný hmotný bod je dané princípom superpozície (vektorového sčítania), ktorý hovorí:
Výsledná sila aj intenzita gravitačného poľa vytvoreného viacerými hmotnými bodmi sú dané súčtom síl, resp. intenzít gravitačných polí jednotlivých hmotných bodov.
V prípade poľa, vytvoreného spojitou sústavou hmotných bodov, resp. telesom (obr. 3.2.3.2b) o celkovej hmotnosti M a objeme V prejdú sumácie v predchádzajúcich vzťahoch do integrácií. Dostaneme tak
a
kde dM a dV sú hmotnostný a objemový element telesa a r je jeho hustota.
Kontrolné otázky
-
Definujte veličinu intenzita gravitačného poľa. V akých jednotkách ju vyjadrujeme?
-
Ktorej veličine sa číselne rovná intenzita gravitačného poľa v danom bode? Vysvetlite, prečo.
-
Ako sa nazývajú krivky, začínajúce v nekonečne a končiace v zdrojoch gravitačného poľa? Akú orientáciu voči takejto krivke má vektor intenzity gravitačného poľa?
-
Čo je to homogénne a nehomogénne gravitačné pole?
-
Čo hovorí princíp superpozície?
