 Gradient skalárnej funkcie
Gradient skalárnej funkcie
V tomto paragrafe bude opísaná derivácia skalárnej funkcie podľa priestorových premenných. Nech je v karteziánskej súradnicovej sústave zadaná skalárna funkcia P(x,y,z), napríklad elektrostatický potenciál. Hodnoty tejto funkcie sa menia, ak postupujeme v smere jednotlivých súradnicových osí, pričom strmosť zmeny nemusí byť vo všetkých smeroch rovnaká. Pod strmosťou zmeny rozumieme prírastok hodnoty funkcie pripadajúci na posunutie v príslušnom smere o jednotku dĺžky (1 meter). Strmosti v smere osí x, y, z označíme symbolmi Sx , Sy , Sz pričom pre ne platí
Limity vo výrazoch pre strmosť predstavujú derivácie. Pri posunutí pozdĺž osi y sa mení len súradnica y , ostatné dve zostávajú nemenné. Takáto derivácia funkcie viacerých premenných sa nazýva parciálna a označuje sa inak ako derivácia funkcie jednej premennej. Strmosť zmien funkcie P(x,y,z) sa vyjadruje potom v tvare:
 (1.3.4.2)
(1.3.4.2)Strmosti Sx , Sy , Sz nie sú v celom priestore konštantné, ale sa môžu od bodu k bodu meniť.
Ak postúpime v smere osi y o Dy , zmení sa hodnota funkcie P(x,y,z) o hodnotu:
(DP)y = Sy Dy = (¶P/¶y) Dy (1.3.4.3)
Ak vykonáme posunutie všeobecným smerom, možno ho rozložiť na tri posunutia v smeroch súradnicových osí, takže celková zmena funkcie P(x,y,z) bude
DP = (DP)x + (DP)y + (DP)z = (¶P/ ¶x) Dx + (¶P/¶ y) Dy + (¶P/¶ z) Dz (1.3.4.4)
alebo pri limitne malých posunutiach :
dP = (¶P/¶ x) dx + (¶P/¶ y) dy + (¶P/¶ z) dz (1.3.4.5)
Takýmto vzťahom je vyjadrený úplný (totálny) diferenciál funkcie troch priestorových premenných. Vzťah (1.3.4.5) možno vyjadriť ako skalárny súčin dvoch vektorov:
diferenciálu polohového vektora
dr = dx i + dy j + dz k (1.3.4.6)
a vektora, ktorý nazývame gradient skalárnej funkcie P:
grad P(x,y,z) = (¶P/¶x) i + (¶P/¶y) j + (¶P/¶z) k (1.3.4.7)
O správnosti tohoto tvrdenia sa čitateľ môže presvedčiť vykonaním skalárneho súčinu. Vektor grad P má smer najstrmšieho vzrastu funkcie P a jeho veľkosť sa rovná tomuto vzrastu, t.j. prírastku funkcie P pripadajúcemu na posunutie o jednotku vzdialenosti. Na ilustráciu - v danom mieste mapy by tento vektor bol kolmý na vrstevnice a veľkosťou by predstavoval prírastok nadmorskej výšky pri posunutí o jednotku vzdialenosti v príslušnom horizontálnom smere.
Výraz grad P sa zapisuje v symbolickom tvare:
grad P = ( i ¶ /¶x + j ¶ /¶ y + k ¶ /¶z) P, (1.3.4.8)
pričom výraz v zátvorke predstavuje diferenciálno - vektorový operátor, nazývaný nabla operátor a označovaný symbolom Ñ:
Ñ = ( i ¶ /¶x + j ¶ /¶y + k ¶ /¶z) (1.3.4.9)
Jeho aplikáciou na skalárnu funkciu podľa vzoru (1.3.4.7) vznikne zo skalárnej funkcie vektorová funkcia. Aplikovať operátor znamená vykonať operácie, ktoré predpisuje. To znamená, že podľa vzťahu (1.3.4.7) treba skalárnu funkciu najprv parciálne derivovať podľa premennej x a týmto výsledkom (skalárom) násobiť jednotkový vektor i . K tomuto členu - prvej zložke výsledného vektora - pripočítať druhý a tretí člen, ktoré dostaneme analogicky, deriváciami podľa premenných y a z , ktorými vynásobíme jednotkové vektory j a k .
Príklad 1.3.4.1
Vypočítajte gradient skalárneho elektrostatického potenciálu v okolí bodového náboja Q , umiestneného v začiatku súradnicovej sústavy. Potenciál je vyjadrený vzťahom V(x,y,z) = K (x2 + y2 + z2)-1/ 2 , kde K = (Q / 4peo).
Riešenie
Najprv vypočítame parciálnu deriváciu potenciálu podľa premennej x:
¶V/¶x = K (-1/2)(x2 + y2 + z2)-3/2 (2x) = - K x (x2 + y2 + z2)-3/2
Výsledky parciálnych derivácií podľa premenných y a z sú analogické, takže môžeme priamo napísať grad V , keď k výsledkom derivácií dopíšeme jednotkové vektory :
|
|
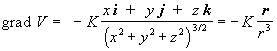 (1.3.4.10)
(1.3.4.10)kde r = xi + yj + zk je polohový vektor miesta v ktorom počítame vektor grad V a v menovateli je tretia mocnina veľkosti polohového vektora. Vektor grad V má opačný smer ako polohový vektor r , lebo elektrostatický potenciál s rastúcou vzdialenosťou od náboja klesá, takže smer vzrastu potenciálu, a teda vektora grad V je opačný.
Gradient vektorovej funkcie predstavuje aplikáciu nabla operátora na vektorovú funkciu. Napríklad grad B(x,y,z) = ( i ¶ /¶ x + j ¶ /¶y + k ¶ /¶ z) B = i ¶ B/¶x + j ¶ B/¶y + k ¶ B/¶ z, pričom len výraz j ¶ B/¶ y = j (¶ Bx / ¶ y i + ¶ By /¶ y j + ¶ Bz /¶ y k ) obsahuje tri členy. Spolu v celom grad B je deväť členov v ktorých však vzťahy medzi vektormi v nich vystupujúcimi sme zatiaľ nedefinovali. Ide o tzv. tenzorovú veličinu, ktorej v tomto texte ďalšiu pozornosť nevenujeme.
Kontrolné otázky
-
Vyjadrite totálny diferenciál skalárnej funkcie priestorových premenných x, y, z !
-
Uveďte, čo je gradient skalárnej funkcie priestorových premenných !
-
Čo predstavujú súradnice (zložky) gradientu skalárnej funkcie ?
-
Napíšte nabla operátor ! Je to skutočný vektor ? Má veľkosť a smer ?
