 Pohyb a poloha hmotného bodu
Pohyb a poloha hmotného bodu
Pod hmotným bodom resp. časticou rozumieme teleso, ktorého rozmery a tvar môžeme pri riešení danej úlohy zanedbať. Jedno a to isté teleso môžeme, podľa toho akú úlohu chceme riešiť, považovať raz za hmotný bod (časticu), inokedy zase za teleso konečných rozmerov.
Pri skúmaní pohybu, pod ktorým rozumieme premiestňovanie telesa, musíme toto premiestňovanie vzťahovať na určité iné teleso. Teleso, vzhľadom na ktoré budeme pohyb popisovať, nazývame vzťažné teleso. Umiestnime ho do počiatku súradnicovej sústavy.
Mechanický pohyb vo všeobecnosti môže vyzerať veľmi rozmanito. Existujú dva jednoduché typy mechanického pohybu: translačný pohyb hmotného bodu (častice) po priamke a rotačný pohyb po kružnici, ktoré majú tú vlastnosť, že akýkoľvek mechanický pohyb možno rozložiť na konečný počet týchto dvoch pohybov. Obidvom venujeme osobitné paragrafy.
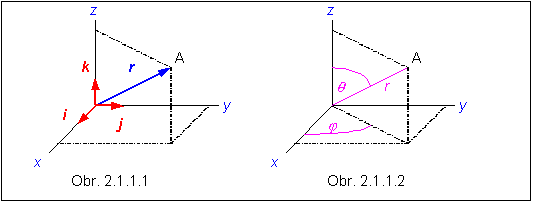
Ak chceme popísať pohyb, musíme v každom časovom okamihu poznať polohu bodu. Polohu bodu v trojrozmernom priestore určujeme najčastejšie karteziánskymi súradnicami x, y, z (bod A na obr. 2.1.1.1). Rovnocenné je určenie polohy polohovým vektorom
r = xi + yj + zk, (2. 1.1.1)
kde i , j , k sú jednotkové vektory rovnobežné so súradnicovými osami karteziánskej súradnicovej sústavy a x, y, z príslušné karteziánske súradnice. Vektory i, j, k tvoria bázu tejto sústavy. Súradnice polohového vektora, a teda vektor r pri pohybe častice sa postupne menia, sú funkciami času : r(t) = x(t) i + y(t) j + z(t) k . Polohový vektor možno rozložiť do zložiek v tvare
r = r x + ry + r z, (2.1.1.2)
kde veľkosť polohového vektora je určená vzťahom
Používanie karteziánskej sústavy nie je vždy optimálne. Napríklad pri opise sústav s guľovou symetriou, je výhodné použiť sférickú súradnicovú sústavu, v ktorej sa používajú sférické súradnice s označením r ,q ,j . Pritom r predstavuje vzdialenosť bodu od začiatku súradnicovej sústavy, q uhol medzi polohovým vektorom r a osou z , a j uhol medzi osou x a priemetom vektora r do roviny (xy). Súradnice vidno na obrázku 2.1.1.2, na základe ktorého možno overiť vzťahy medzi karteziánskymi a sférickými súradnicami bodu A
z = r cosq , y = r sinq sinj , x = r sinq cosj (2.1.1.4)
a opačne:
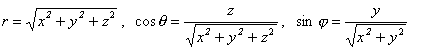 (2.1.1.5)
(2.1.1.5)Kontrolné otázky
-
Ako je definovaná karteziánska súradnicová sústava?
-
Čo je bázou karteziánskej súradnicovej sústavy?
-
Ktoré premenné veličiny určujú sférickú súradnicovú sústavu?
-
Napíšte vzťah medzi súradnicami karteziánskej a sférickej súradnicovej sústavy.
-
Vyjadrite polohový vektor súradnicovej sústavy v zložkovom tvare.
-
Vyjadrite polohový vektor ako súčet priemetov vektora r do jednotlivých osí karteziánskej súradnicovej sústavy.
-
Napíšte vzťah pre veľkosť polohového vektora.
-
Ktorá časť mechaniky sa zaoberá len opisom pohybu?
-
Čo je predmetom štúdia kinematiky?
-
Čo je predmetom štúdia dynamiky?
-
Akou rýchlosťou sa môže pohybovať hmotný bod, resp. teleso, aby sme jeho pohyb skúmali pomocou klasickej mechaniky?
-
V akých prípadoch pohyb musíme skúmať pomocou relativistickej mechaniky?
-
Ktorá časť mechaniky sa zaoberá skúmaním zákonitostí v oblasti mikrosveta?
-
Ktorá časť mechaniky sa zaoberá podstatou pohybu a príčinou vzniku pohybov?
-
Definujte pojem vzťažná sústava.
-
Definujte pojem hmotný bod a uveďte príklady, kedy môžeme teleso považovať za hmotný bod.
-
Aké základné dva druhy mechanického pohybu rozlišujeme?
-
V akých vzťažných sústavách najčastejšie skúmame pohyb?
-
Definujte pojem polohový vektor hmotného bodu a napíšte jeho matematické vyjadrenie. Vysvetlite význam jednotlivých veličín.
