 Rozklad kmitov, harmonická analýza
Rozklad kmitov, harmonická analýza
Opakom skladania kmitov rovnakého smeru je rozklad kmitov na násobky základnej frekvencie – Fourierova analýza. Fourierova analýza má veľký praktický význam, a to hlavne v oblasti analýzy zvukov, spracovania impulzných signálov, ako aj v moderných spektroskopických prístrojoch.
Podľa Fourierovej vety každú periodickú funkciu s periódou T a s konečným počtom nespojitostí možno vyjadriť v tvare
kde w = 2p/T a konštanty A0, Ak, Bl sú určené rovnicami
Platnosť týchto vzťahov si ľahko overíme ak využijeme vzťahy známe z integrálneho počtu a to
Ak budeme integrovať rovnicu (6.1.9.1) v intervale <0, T>, všetky členy okrem A0 na pravej strane tejto rovnice vypadnú a dostávame tvrdenie (6.1.9.2). Ak rovnicu (6.1.9.1) vynásobíme cos(kw t) a integrujeme v rovnakom intervale vypadnú všetky členy v ktorých vystupuje funkcia sin a nenulový bude iba člen pri Ak, z čoho priamo vyplýva tvrdenie (6.1.9.3). Rovnicu (6.1.9.4) dostávame analogicky, ak (6.1.9.1) vynásobíme sin(lw t) a integrujeme v intervale <0, T>. Čím väčší počet členov v rozvoji (6.1.9.1) zoberieme do úvahy, tým presnejšie reprodukujeme pomocou harmonických funkcií periodickú funkciu f(t).
Príklad 6.1.24
Rozložte jednotkovú periodickú funkciu f(t), znázornenú na obr.6.1.17 do harmonických zložiek.
Riešenie
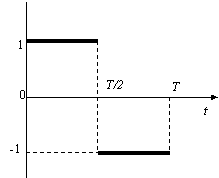
Matematicky vyjadríme danú funkciu nasledovne:
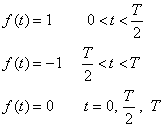
Pre funkciu f(t) platí:
Hľadáme amplitúdy A0, Ak, Bk:
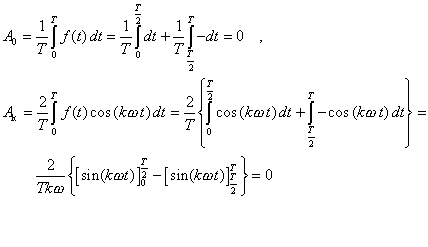
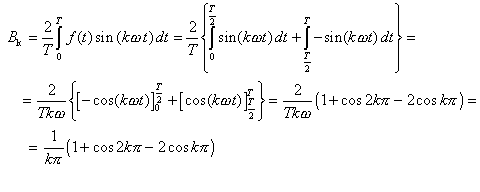
Pre nepárne hodnoty k = 1, 3, 5, 7, ... dostaneme
pre párne = 2, 4, 6, ... je B k = 0.
Hľadaný rozvoj funkcie bude mať tvar:
