 Dopplerov jav
Dopplerov jav
Z bežného vnímania výšky tónu pohybujúceho sa zdroja, napr. zvuku trúbiaceho auta vieme, že tón je vyšší, ak sa zdroj pohybuje k nám a nižší, ak sa zdroj zvuku pohybuje od nás. Zmena frekvencie vnímaného tónu je príkladom Dopplerovho javu. Dopplerov jav je závislosť prijímanej frekvencie vlnenia na pohybe pozorovateľa, alebo pohybe zdroja. Hans Christian Doppler objavil tento jav v roku 1842 a nepozorujeme ho iba pri zvuku. Prejavuje sa pri všetkých vlnových dĺžkach elektromagnetického vlnenia, teda aj pri svetle. Na základe Dopplerovho javu môže polícia merať rýchlosť automobilu radarom a pod. .
Majme zdroj vysielajúci zvukové vlny frekvencie f, ktoré v danom prostredí vytvárajú vlnenie s vlnovou dĺžkou l = v/f. Vyšetrime najprv prípad pohybu pozorovateľa.
Pohyb pozorovateľa. Nech je zdroj vlnenia v pokoji a pozorovateľ sa k nemu pohybuje rýchlosťou vp. Kružnice na obr.6.2.9 (a) reprezentujú vlnoplochy (hrebene vĺn) medzi ktorými je vzdialenosť l. Ak by bol pozorovateľ v pokoji, za čas t by zaregistroval, že okolo neho prešiel počet vt/l vĺn, kde v je rýchlosť šírenia sa vlnenia. Vzhľadom na to, že sa pohybuje smerom k zdroju „stretne“ pri svojom pohybe za čas t ešte naviac vp t/l vĺn. Frekvencia, ktorú bude počuť pozorovateľ sa rovná počtu zaregistrovaných maxím za časovú jednotku
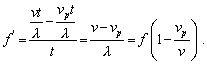 (6.2.8.1)
(6.2.8.1)Ak sa pozorovateľ pohybuje od zdroja rýchlosťou vp < v , tak zaregistruje menší počet vĺn a počuje frekvenciu
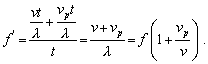 (6.2.8.2)
(6.2.8.2)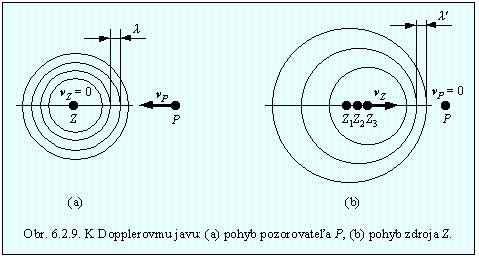
Pohyb zdroja. Nech sa zdroj vlnenia kmitajúci s frekvenciou f pohybuje smerom k pozorovateľovi rýchlosťou vz., obr.6.2.9(b). Vzdialenosť vlnoplôch s rovnakou fázou sa v dôsledku pohybu zdroja medzi zdrojom a pozorovateľom zmenší a bude sa rovnať
Frekvencia vlnenia, ktorú zaregistruje pozorovateľ, je daná počtom prejdených maxím za časovú jednotku a rovná sa
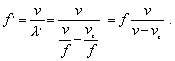 (6.2.8.4)
(6.2.8.4)Ak sa bude zdroj pohybovať od pozorovateľa vlnová dĺžka sa zväčší l’ = l + vzT a pozorovateľ zaregistruje v takomto prípade frekvencie
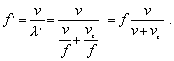 (6.2.8.5)
(6.2.8.5)V prípade, že sa pohybuje aj zdroj aj pozorovateľ frekvenciu vlnenia získame rovnakým postupom a bude sa rovnať
kde horné znamienko platí pre prípad, keď sa zdroj a pozorovateľ pohybujú proti sebe, dolné znamienko platí pre prípad, keď sa pohybujú od seba. Ľahko si znamienka zapamätáte, keď si uvedomíte, že pri pohybe smerom k sebe počujeme frekvenciu vyššiu.
Pôvodná Dopplerova práca z r. 1842 sa zaoberala zmenou farby svetla vyžarovaného pohybujúcim sa zdrojom. Dnes vieme, že svetlo k svojmu šíreniu nepotrebuje žiadne prostredie, rýchlosť svetla je vždy konštantná a nezávisí na pohybe zdroja ani pozorovateľa. Tu ukázané odvodenie Dopplerovho javu nie je pre svetlo korektné.
Dopplerov jav sa využíva v mnohých oblastiach, 1nielen pri meraní rýchlosti áut. Napr. moderné vyšetrovacie metódy v medicíne dokážu na základe tohoto javu merať rýchlosť prietoku krvi. Jedna zo spektroskopických metód používaných na štúdium molekulových komplexov – Mössbauerova spektroskopia je založená tiež na tomto jave. Gigantickým prejavom Dopplerovho javu je takzvaný červený posun (k väčším vlnovým dĺžkam) spektier vzdialených galaxií. Čím je galaxia od nás ďalej, tým je posun väčší. Znamená to, že sa vzďaľuje rýchlejšie a to je pre astrofyziku jedným z experimentálnych dôkazov „big bandu“ – počiatočnej explózie vesmíru.
Príklad 6.2.9
Zdroj zvuku kmitá s frekvenciou f = 1 kHz. Rýchlosť zvuku vo vzduchu je v = 340 m s–1. Určte, akú frekvenciu počuje pozorovateľ a aká je vlnová dĺžka zvuku vo vzduchu, ak
(a) pozorovateľ je vzhľadom na vzduch v pokoji a zdroj sa k nemu približuje rýchlosťou vz = 30 m s–1,(b) zdroj je vzhľadom na vzduch v pokoji a pozorovateľ sa k nemu približuje rýchlosťou vp = 30 m s–1.
Možno z výsledku vyvodiť záver, že pri určovaní frekvencie nie je dôležité vedieť, či sa pohybuje zdroj alebo pozorovateľ, ale stačí poznať iba ich vzájomnú rýchlosť?
Riešenie
Ide tu o Dopplerov jav. Frekvencia, ktorú počuje pozorovateľ v prípade (a) je daná vzťahom (6.2.8.4)
Pre vlnovú dĺžku v priestore medzi pozorovateľom a zdrojom platí (6.2.8.3) a
(b) Pohybuje sa pozorovateľ k zdroju. Frekvencia, ktorú počuje pozorovateľ je daná vzťahom (6.2.8.1)
Vlnová dĺžka zvuku je v tomto prípade
Vzájomná rýchlosť zdroja a pozorovateľa je v prípade (a) a (b) rovnaká, výsledná frekvencia vnímaná pozorovateľom je však rôzna (i keď v oboch prípadoch vyššia než frekvencia zdroja). To znamená, že pri riešení úlohy je samotná informácia o vzájomnej rýchlosti nedostatočná. Treba spresniť, či sa pohybuje zdroj alebo pozorovateľ.
Príklad 6.2.10
Z nehybného zdroja sa šíri zvuk s frekvenciou f = 500 Hz a odráža sa od pohyblivej steny, ktorá sa k zdroju približuje rýchlosťou vs = 1 m s–1. Určte vlnovú dĺžku odrazeného zvuku. Rýchlosť zvuku je v = 340 m s–1.
Riešenie
Pohybujúca sa stena vystupuje ako pozorovateľ pohybujúci sa k zdroju. Stena prijíma frekvenciu určenú vzťahom (6.2.8.1)
Pre odrazený zvuk stena vystupuje ako pohybujúci sa zdroj, ktorý vysiela zvuk frekvencie f'. Vlnová dĺžka odrazeného zvuku bude v dôsledku pohybu zdroja vzhľadom k prostrediu zmenšená a to o vzdialenosť d = vs / f '. Ak označíme vlnovú dĺžku, ktorú by malo vlnenie frekvencie f' vysielané nepohyblivým zdrojom ako l', potom vlnová dĺžka odrazeného zvuku je
