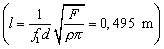Odraz a lom vlnenia
Odraz a lom vlnenia
Pre odraz a lom vlnenia platia tieto zákony:
1. Uhol dopadu sa rovná uhlu odrazu.2. Na rozhraní dvoch prostredí sa vlnenie láme tak, že podiel sinusov uhla dopadu a uhla lomu sa rovná podielu rýchlostí vlnenia v týchto prostrediach.
Obidva zákony si dokážeme využitím Huygensovho princípu. Nech rovinná vlna dopadá na odrazovú plochu pod uhlom a (obr. 6.2.10).
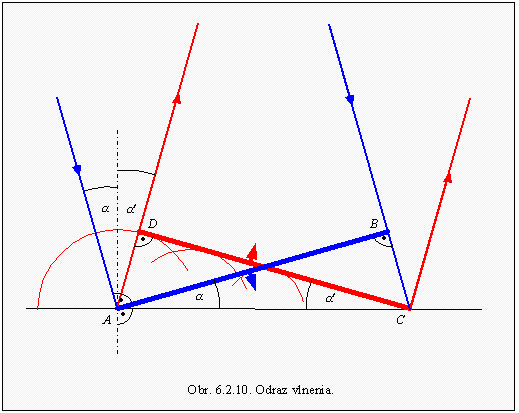
Uhol dopadu je uhol, ktorý zviera dopadajúci lúč s kolmicou dopadu. Analogicky je definovaný uhol odrazu. Na obr. 6.2.10 je AB vlnoplocha dopadajúcej vlny v čase t, keď na rozhranie dopadá lúč do bodu A, CD je vlnoplocha odrazeného vlnenia, a to v čase t + Dt, keď na rozhranie dopadol lúč do bodu C. Všetky body rozhrania sa podľa Huyghensovho princípu stávajú postupne (ako do nich dostúpi čelo rovinnej vlny) zdrojmi vlnenia. Polomer elementárnej vlnoplochy vytvorenej po dopade lúča do bodu A sa za tento čas rovná vDt. Vzhľadom na to, že dopadajúci aj odrazený lúč sa pohybujú rovnakými rýchlosťami, AD = v Dt = BC a pre uhly a a a’ z obrázku 6.2.10. platí sina = BC /AC = AD/AC=sina’, odkiaľ vyplýva a = a’ t.j. uhol dopadu sa rovná uhlu odrazu.
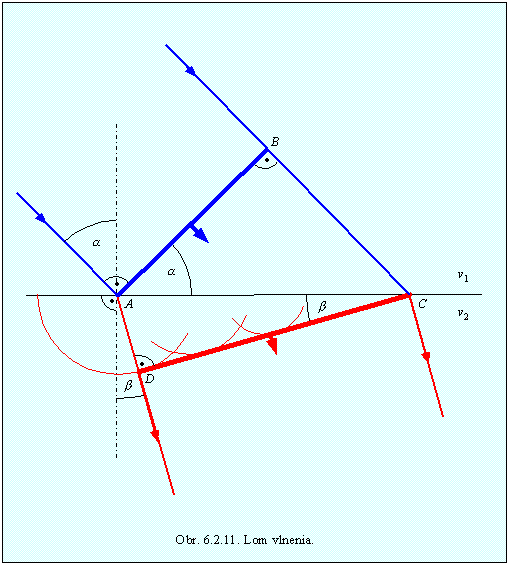
Dokážme teraz zákon lomu. Nech rýchlosť vlnenia v prostredí 1 je v1 a v prostredí 2 je v2. (obr.6.2.11 ). Za čas Dt, o ktorý dopadne lúč na rozhranie do bodu C neskôr ako dopadol lúč do bodu A, prejde čelo rovinnej vlny v prostredí 1 dráhu BC = v1Dt. Lúč, ktorý dopadol do bodu A, prechádza do druhého prostredia a prejde v ňom za tento čas dráhu AD = v2Dt.
Podľa obr 6.2.11 platí
takže
kde n12 je konštanta charakterizujúca dané rozhranie a nazývame ju relatívny index lomu.
Rovnica (6.2.9.1) vyjadruje Snellov zákon lomu. Ak je rýchlosť vlnenia v prostredí 2 menšia ako v prostredí 1 hovoríme, že nastáva lom ku kolmici, ak je rýchlosť v prostredí, do ktorého sa vlnenie láme väčšia hovoríme, že nastáva lom od kolmice. Ak nastáva lom od kolmice, potom existuje taký uhol dopadu, pri ktorom sinb = 1. Tento uhol voláme medzný uhol a pre tento uhol platí sinam = n12. Ak bude uhol dopadu taký, že sina > n12 vlnenie z prostredia 1 neprenikne do prostredia 2 a nastáva úplný odraz.
V optike sa zavádza absolutný index lomu n = c/v, je to podiel rýchlosti svetla v danom prostredí a rýchlosti svetla vo vákuu. Snellov zákon má potom tvar
sina n1 = sinb n2 (6.2.9.2)
Príklad 6.2.10
Pod akým uhlom a vzhľadom na kolmicu musí dopadať zvuk na hladinu vody, aby sa ďalej vo vode šíril pod uhlom b = 45°? Rýchlosť zvuku vo vzduchu je v1 = 340 m s–1, vo vode v2 = 1 450 m s–1.
Riešenie
Platí zákon lomu
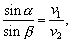
odkiaľ
Príklad 6.2.11
Pod akým najväčším uhlom vzhľadom na kolmicu môže dopadať zvuková vlna na rozhranie vzduchu a vody, aby prenikla do vody? Rýchlosť zvuku vo vzduchu je v1 = 340 m s–1, vo vode v2 = 1 450 m s–1.
Riešenie
Pri prechode do vody sa smer zvuku láme od kolmice. Pre najväčší (medzný) uhol, pri ktorom zvuk ešte prenikne do vody a nenastáva úplný odraz, platí
odkiaľ potom pre hľadaný uhol platí
Kontrolné otázky
-
V čom je rozdiel medzi kmitaním hmotného bodu a vlnením?
-
Čo sa rozumie pojmom polarizácia vlnenia?
-
Čo vyjadruje vlnová funkcia?
-
Čo je vlnová dĺžka a čo vyjadruje uhlové vlnové číslo?
-
Ako zistíme, či daná funkcia opisuje vlnenie, t. j. či je vlnovou funkciou?
-
Aký je rozdiel medzi fázou a fázovou konštantou?
-
Aký je vzťah medzi vlnovou funkciou a vlnovou rovnicou?
-
Čo znamená pojem koherentnosť dvoch vlnení?
-
Kedy sa interferujúce vlnenia najviac zosilujú a kedy sa najviac zoslabujú?
-
Akú podmienku musia spĺňať dve navzájom kolmé lineárne polarizované priečne vlnenia, aby vzniklo lineárne polarizované vlnenie?
-
Akú podmienku musia spĺňať dve navzájom kolmé lineárne polarizované vlnenia, aby vzniklo kruhovo polarizované vlnenie?
-
Pri akých podmienkach vzniká stojaté vlnenie?
-
Aké frekvencie stojatého vlnenia môžu vzniknúť na napnutej strune dĺžky l?
-
Čo je Dopplerov jav? Nakreslite k nemu vysvetľujúci obrázok a napíšte vzťah, ktorý ho vyjadruje.
-
Vyjadrite intenzitu mechanického vlnenia. Aký je rozmer intenzity vlnenia?
-
Nakreslite schematický obrázok stojatého vlnenia na napnutej strune pre základnú harmonickú a vyššie harmonické.
-
Nakreslite schematický obrázok stojatého vlnenia vo vzduchovom stĺpci v trubici, ktorá je na jednom konci zatvorená a na druhom otvorená. Obrázok nakreslite pre základnú harmonickú a vyššie harmonické.
-
Vysvetlite rozdiel medzi fázovou a grupovou rýchlosťou vlnenia.
-
Ako sa volá závislosť fázovej rýchlosti vlnenia od vlnovej dĺžky?
-
Ako sa zmení vnímaná frekvencia vlnenia na vodnej hladine, ak sa budeme na člne pohybovať (a) proti smeru šírenia vlnenia, (b) v smere šírenia vlnenia?
-
Zdroj harmonického vlnenia sa pohybuje po priamke konštantnou rýchlosťou, ktorá je nižšia než fázová rýchlosť vlnenia. Je vlnová dĺžka vlnenia za zdrojom a pred zdrojom rovnaká? Ak nie, kde je väčšia?
-
Ako sa zmení (stačí vyriešiť kvalitatívne) frekvencia zvuku, ktorý vníma pozorovateľ, ak sa zdroj (a) vzďaľuje od nepohyblivého pozorovateľa, (b) približuje k nepohyblivému pozorovateľovi?
-
Je vlnenie po odraze na nepohyblivej prekážke koherentné s dopadajúcim vlnením? Ako je to v prípade odrazu na pohybujúcej sa prekážke?
-
Ako sa láme smer šírenia vlnenia pri prechode z prostredia s menšou fázovou rýchlosťou do prostredia s väčšou fázovou rýchlosťou: ku kolmici alebo od kolmice?
-
Svetlo je vlnenie. Rýchlosť šírenia svetla vo vzduchu je vyššia ako vo vode. Čo vidíme, keď sme pod vodou a dívame sa zdola na pokojnú hladinu?
-
Ako sa nám javí palica ponorená kolmo do vody, keď sa na ňu dívame sponad hladiny zo vzduchu: kratšia alebo dlhšia?
Príklady
6.2.12 Po napnutej strune sa šíri priečne vlnenie, ktoré možno opísať vlnovou funkciou u = a sin (b x + c t), kde a = 0,06 m, b = 2p m–1, c = 4p s–1. Určte pre toto vlnenie amplitúdu, (b) vlnovú dĺžku, (c) uhlovú frekvenciu a frekvenciu, (d) periódu, (e) vlnové číslo, (f) rýchlosť šírenia (fázovú rýchlosť), (g) smer (orientáciu) šírenia, (h) maximálnu rýchlosť bodu na strune.( (a)A = a =0,06 m ; (b) k = b = 2p m–1 ; (c) w = c = 4p s–1; (d) f = c /2p = 2 Hz; (e) T = 2p /c = 0,5 s; (e) l = 2p /b =1 m; (f) v = c/b =2 m.s-1; (g) orientácia proti smeru x, (h) vmax = ca = 0,24 p m.s-1 .)6.2.13 Vo vzduchu sa šíri harmonické zvukové vlnenie s frekvenciou f = 500 Hz. Rýchlosť šírenia vlnenia je 340 m s–1. Určte: (a) vzdialenosť medzi bodmi, ktoré kmitajú s fázovým rozdielom Df = 60o, (b) fázový rozdiel výchyliek daného bodu v dvoch okamihoch, medzi ktorými je časový rozdiel Dt = 10–3 s.( a) Dx = 0,113 m, (b) Dj = p rad )6.2.14 Ukážte, že komplexná funkcia u(t,x) = Aei (at-kx) je riešením jednorozmernej aj trojrozmernej vlnovej rovnice. Určte fázovú rýchlosť a tvar vlnoplochy tohto vlnenia.
( v = w / k, vlnoplochy sú kolmé na os x).6.2.15 Ukážte, že každá diferencovateľná funkcia f(t – ax ) , kde a je konštanta, je riešením vlnovej rovnice. Aký je fyzikálny zmysel konštanty a ?(a = 1/v, kde v je fázová rýchlosť).6.2.16 Ukážte, že vlnoplocha vlnenia opisovaného vlnovou funkcioukde w, k sú konštanty, t je čas a r je vzdialenosť bodu od zdroja vlnenia, je guľa, takže táto funkcia opisuje guľovú vlnu. Určte fázovú rýchlosť tohto vlnenia. ( Pre vlnoplochu platí r = konšt, a to je rovnica guľovej plochy; fázová rýchlosť n =w / k. )6.2.17 Pre veľmi krátke vlny, ktoré vznikajú na vodnej hladine v dôsledku povrchového napätia, je disperzia daná vzťahomkde v je fázová rýchlosť vlnenia, l je vlnová dĺžka, s je povrchové napätie a r je hustota kvapaliny. Určte grupovú rýchlosť tohto vlnenia.6.2.18 Oceľový drôt s priemerom r = 1 mm je napínaný silou F = 50 N. Po drôte sa šíri harmonické vlnenie s vlnovou dĺžkou l = 0,3 m a s amplitúdou A = 1 mm. Určte maximálnu priečnu rýchlosť bodov na drôte. Hustota ocele je r = 7 800 kgm–3.6.2.19 Dve priečne harmonické vlnenia s amplitúdami A1 a A2 , polarizované v dvoch vzájomne kolmých rovinách, sa šíria po strune rovnakým smerom rovnakou rýchlosťou. Určte, ako bude polarizované výsledné vlnenie, ktoré vzniká ich interferenciou, ak (a) A1 = A2 a vlnenia majú rovnakú fázu, (b) A1 = 2 A2 a fázový rozdiel medzi vlneniami je p/2, (c) A1 = A2 a fázový rozdiel medzi vlneniami je p/2.( a) lineárne, b) elipticky, c) kruhovo.)6.2.20 Dĺžka l prvku televíznej antény sa približne rovná vzdialenosti medzi dvoma uzlami stojatého elektromagnetického vlnenia vo vákuu. Určte dĺžku l antény určenej na príjem 1. televízneho kanála. (f1 » 52 MHz) a 60. televízneho kanála(f2 » 786 MHz).( l = c/ f ; l1 = 2,88 m ; l2 = 0,191 m ).6.2.21 Určte silu, ktorou treba napínať strunu s hmotnosťou m = 1 g a s dĺžkou l = 250 mm, aby základná frekvencia jej kmitania bola fo = 1 kHz.(F = 4lmf12 = 103 N.)6.2.22 Oceľová struna s priemerom d = 0,1 mm je napínaná silou F = 60 N. Aká musí byť dĺžka struny, ak chceme, aby základná frekvencia jej kmitov bola fo = 1 kHz? Hustota ocele je r = 7800 kg m–3.6.2.23 Po strune sa proti sebe z dvoch zdrojov šíria rovnakou rýchlosťou a vzájomne interferujú dve harmonické vlnenia. Zdroje majú rovnakú amplitúdu A a kmitajú vo fáze. Určte amplitúdu kmitania bodu, ktorý sa nachádza v strednej vzdialenosti medzi zdrojmi.6.2.24 Na strune sa nachádzajú dva koherentné zdroje vlnenia, ktoré kmitajú v protifáze s amplitúdou A. Určte amplitúdu kmitania bodu, ktorý sa nachádza v strede úsečky spájajúcej zdroje.6.2.25 Určte možné frekvencie zvuku, ktorý vydávajú uzavretá a otvorená organová píšťala s dĺžkou l = 1 m. Rýchlosť zvuku je v = 340 m s–1. (Na konci s kmitajúcim jazýčkom sa v oboch prípadoch vytvorí kmitňa).Pre uzavretú,
6.2.26 Určte tri najnižšie harmonické zložky zvuku píšťalky s dĺžkou l = 100 mm s uzavretým koncom. Rýchlosť zvuku je v = 340 m s–1. (Na konci s kmitajúcim jazýčkom sa vytvorí kmitňa.)( f = (2n + 1) v / 4l , kde n = 0,1,2,; f0 =850 Hz ; f1 = 2550 Hz ;f2 = 4250 Hz .)6.2.27 V Kundtovej trubici naplnenej vodíkom sme vytvorili stojaté vlnenie pomocou oceľovej tyče s dĺžkou l = 1,2 m. Vzdialenosť medzi susednými uzlami stojatého vlnenia, zistená meraním, je Dx = 288 mm. Rýchlosť zvuku v oceli je v´ = 5 300 m s–1. Určte rýchlosť zvuku vo vodíku.6.2.28 Pomocou mosadznej tyče dĺžky l = 1 m upevnenej v strede sme v Kundtovej trubici vytvorili stojaté vlnenie. Vzdialenosť susedných uzlov stojatého vlnenia bola Dx = 0,1m. Určte rýchlosť zvuku v mosadznej tyči ak rýchlosť zvuku vo vzduchu je v = 340 m s–1.6.2.29 Píšťala rušňa, ktorý sa vzďaľuje zo stanice, vydáva zvuk s frekvenciou f = 500 Hz. Človek stojaci na stanici počuje frekvenciu zvuku f’ = 472 Hz . Určte, akou rýchlosťou sa vlak vzďaľuje zo stanice. Rýchlosť zvuku je v = 340 m s–1.6.2.30 Píšťalka vydávajúca zvuk s frekvenciou f = 1 kHz sa pohybuje po kružnici s polomerom R = 0,6 m uhlovou rýchlosťou w = 15 rad s–1. Určte, akú najnižšiu a najvyššiu frekvenciu bude počuť nehybný pozorovateľ. Rýchlosť zvuku je v = 340 m s–1.6.2.31 Dve autá sa pohybujú rovnakým smerom rýchlosťou v1 = 72 km h–1 a vydávajú harmonický zvuk s frekvenciou f = 150 Hz. Medzi nimi sa nachádza nepohyblivý pozorovateľ. Určte frekvenciu rázov, ktoré bude počuť pozorovateľ. Rýchlosť zvuku je v = 340 m s–1.6.2.32 Zvukové vlnenie dopadá zo vzduchu na pokojnú vodnú hladinu pod uhlom j = 45°. Prenikne tento zvuk čiastočne do vody alebo sa úplne odrazí? Rýchlosť zvuku vo vzduchu je v1 = 340 m s–1, vo vode v2 = 1 450 m s–1.(Zvuk sa úplne odrazí, lebo j > am = arcsin v1 / v2 = 13033¢)