 Vektory rýchlosti a zrychlenia pri pohybe po kružnici
Vektory rýchlosti a zrychlenia pri pohybe po kružnici
Je výhodné začiatok súradnicovej sústavy stotožniť so stredom kružnice. Vtedy polohový vektor r častice pohybujúcej sa po kružnici nemení svoju veľkosť. Preto rýchlosť častice vyjadríme pomocou vzorca (2.1.6.1) :
v = dr / dt = w ´ r, (2.1.7.1)
ktorého geometrický význam (vzájomnú orientáciu vektorov) vidno na obr. 2.1.6.1 .
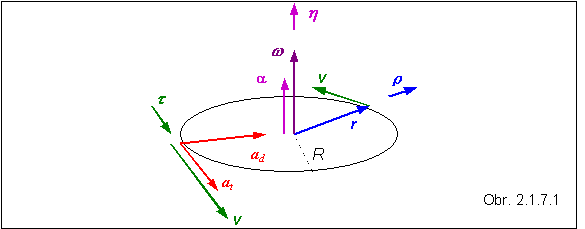
Ak si uvedomíme, že r = R r , kde R je veľkosť polohového vektora r zhodná s polomerom kružnice a r jednotkový vektor, ktorý má smer polohového vektora (obr. 2.1.7.1), možno si vzťah (2.1.7.1) podrobnejšie zdôvodniť takto :
Pritom sme využili skutočnosť, že polomer R kružnice sa s časom nemení, takže dR / dt = 0.
Zrýchlenie a častice pohybujúcej sa po kružnici získame deriváciou jej rýchlosti:
Ako vidno, vektor zrýchlenia má dve zložky . Zložka a t = (a ´ r ) je kolmá na polohový vektor (v ktoromkoľvek časovom okamihu) a súčasne na vektor uhlového zrýchlenia. Má smer dotyčnice kružnice a preto ide o tangenciálnu zložku zrýchlenia. Jej veľkosť je at = Ra , lebo vektory a a r sú na seba kolmé (pozri aj 2.1.5.6). Druhá zložka, ad = w ´ (w ´ r ) sa nazýva dostredivá (alebo normálová) lebo smeruje do stredu kružnice. Jej smer si ľahšie overíme rozpísaním dvojnásobného vektorového súčinu, ktorým je vyjadrená:
ad = w ´ (w ´ r) = w (w × r) - r (w.w) = 0 - rw 2 (2.1.7.4)
Z výsledku dobre vidno, že vektor ad má opačný smer ako polohový vektor r . Pri výpočte sme využili skutočnosť, že vektory w a r sú na seba kolmé, takže skalárny súčin (w × r) = 0.
Tangenciálnu zložku zrýchlenia môžeme vyjadriť v tvare at = at t , kde t je jednotkový vektor súhlasne rovnobežný s vektorom rýchlosti častice. Skalárna veličina at = R (dw /dt) je kladná, ak sa veľkosť uhlovej rýchlosti s časom zväčšuje, v opačnom prípade je záporná. Preto veličina at nepredstavuje veľkosť tangenciálneho zrýchlenia (veľkosť je vždy nezáporná), ale súradnicu tangenciálneho zrýchlenia vzhľadom na jednotkový vektor t.
Ak sa veľkosť vektora rýchlosti častice pri pohybe po kružnici nemení, nemení sa ani veľkosť uhlovej rýchlosti, takže tangenciálne zrýchlenie a uhlové zrýchlenie sa rovnajú nule. Dostredivé zrýchlenie však nie je nulové.
Veľkosť dostredivého zrýchlenia ad = | ad |, vzhľadom na vzťah v = Rw , možno vyjadriť tromi spôsobmi :
ad = Rw 2 = w v = v 2 / R (2.1.7.5)
Zrýchlenie možno rozložiť na dve zložky aj v prípade, že častica sa pohybuje po všeobecnej, zakrivenej dráhe K (obr. 2.1.7.2). Vektor rýchlosti v ľubovoľnom časovom okamihu vyjadríme ako skalárny násobok jednotkového vektora v = v t . Zrýchlenie je jeho deriváciou podľa času:
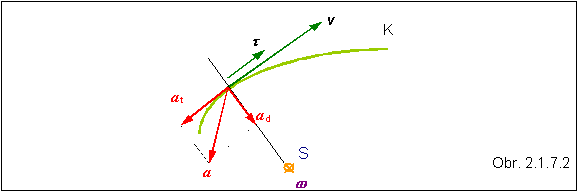
Vidno, že prvá zložka (2.1.7.6) má smer jednotkového vektora t , je jeho skalárnym násobkom, má teda smer dotyčnice krivky, po ktorej sa častica pohybuje a určuje tangnciálne zrýchlenie podľa rovnice
Druhá zložka vo vzťahu (2.1.7.6) má smer vektora vyjadreného vektorovým súčinom (w ´ v) , preto je kolmá na vektor v . Vo vektorovom súčine vystupuje vektor w , ktorý vyjadruje uhlovú rýchlosť otáčania vektora t v danom okamihu. Na obrázku je vektor w znázornený krúžkom s krížikom, čo znamená, že vstupuje do roviny papiera (resp. monitora) . Navyše je umiestnený do stredu krivosti S krivky K , ktorý je stredom oskulačnej kružnice, ktorou možno dostatočne dobre nahradiť príslušný malý úsek krivky . Druhý člen rovnice (2.1.7.6) prezentuje dostredivé zrýchlenie, ktorého veľkosť je určená rovnicou (2.1.7.4).
Vektory tangenciálneho a dostredivého zrýchlenia sú na seba kolmé, celkové zrýchlenie a častice je ich vektorovým súčtom. Preto veľkosť celkového zrýchlenia vypočítame pomocou Pythagorovej vety:
Na obr. 2.1.7.2 je znázornená krivka ležiaca v rovine papiera. Uvedené úvahy však platia aj v prípade, ak krivka neleží v jednej rovine, ale je zakrivená "priestorovo", lebo v ľubovoľnom bode krivky možno jej tromi bodmi, ktoré sú dostatočne blízko pri sebe, preložiť rovinu. (Nazývame ju oskulačná rovina).
Príklad 2.1.7.1
Po opustení stanice rýchlosť vlaku rovnomerne vzrastá a po troch minútach od opustenia stanice dosahuje na dráhe zakrivenej do tvaru kružnice s polomerom R = 800 m hodnotu 72 km.h-1. Určite hodnotu tangenciálneho, normálového a celkového zrýchlenia po dvoch minútach od okamihu opustenia stanice.
Riešenie
Hodnoty známych veličín: R = 800 m, v3 = 72 kmh-1 = 20 ms-1, t3 = 180 , t2 = 120 s .
Rýchlosť rovnomerne vzrastá z nulovej počiatočnej hodnoty zapíšeme vzťahom
v = k¢ t Þ k= v3 / t3.
Pre tangenciálne zrýchlenie na základe vzťahu (2.1.7.7)
Pre normálové zrýchlenie na základe vzťahu (2.1.7.5) platí
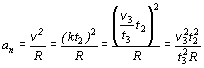
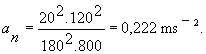
Pre veľkosť celkového zrýchlenia dostávame po dosadení hodnotu
Kontrolné otázky
-
Nakreslite si ľubovolnú trajektóriu hmotného bodu a pre Vami zvolený prípad nakreslite vektor rýchlosti.
-
V sústave SI napíšte jednotku rýchlosti a zrýchlenia.
-
Do akých dvoch smerov je vhodné rozkladať vektor zrýchlenia hmotného bodu?
-
V sústave SI napíšte jednotku uhlovej rýchlosti a uhlového zrýchlenia.
-
Vysvetlite fyzikálny význam normálového zrýchlenia!
-
Napíšte matematické vyjadrenie pre dostredivé zrýchlenie hmotného bodu.
-
Vysvetlite fyzikálny význam tangenciálneho zrýchlenia!
-
Napíšte vzťah pre tangenciálne zrýchlenie hmotného bodu.
-
Napíšte vzťah pre celkové zrýchlenie hmotného bodu.
-
Ak sa hmotný bod pohybuje rovnomerným pohybom, je vždy jeho zrýchlenie nulové?
-
Aké je celkové zrýchlenie hmotného bodu pri rovnomernom pohybe po kružnici?
