 Energia
Energia
V mechanike pod energiou rozumieme veličinu charakterizujúcu pohybový, alebo polohový stav mechanickej sústavy (pod mechanickou sústavou rozumieme časticu ( hmotný bod), sústavu častíc, alebo teleso) s ohľadom na možnosť vykonania práce. Čím viac práce je schopná mechanická sústava vykonať, tým má väčšiu (mechanickú) energiu. Zmena energie sústavy - jej úbytok aj prírastok - sa vyjadruje prácou, ktorú sústava vykoná, resp. ktorú sústave dodáme. Energia je stavová veličina, sústava má energiu, aj keď sa jej stav nemení. O práci možno hovoriť iba vtedy, ak sa stav sústavy mení, s čím súvisí aj zmena jej energia. Vonkajšie sily vykonaním práce môžu napríklad zväčšiť rýchlosť telesa, zodvihnúť ho vyššie, alebo teleso zdeformovať (stlačiť, natiahnuť pružinu) čím teleso získa väčšiu energiu, ktorú potom môžeme využiť na vykonanie práce. Populárnejšie to možno vyjadriť tak, že energia je v sústave "našetrená" práca. Uvedené skutočnosti vyjadrujeme kvantitatívne vzťahom
W = k (E2 - E1) (2.2.5.1)
kde W predstavuje sústave dodanú prácu, E2 a E1 energie konečného resp. začiatočného stavu a k je konštanta, ktorá závisí od voľby jednotiek práce a energie. V sústave SI sa pre tieto dve veličiny používa rovnaká jednotka - joule. Preto konštanta k sa rovná jednotke. Podľa vzorca (2.2.5.1) potom práca dodaná sústave sa číselne rovná zmene energie sústavy.
Uvedieme tri špeciálne prípady mechanickej energie a ich súvislosť s prácou.
A) Kinetická energia
Zo skúsenosti vieme, že keď na voľnú časticu pôsobí sila, urýchľuje ju, zväčšuje jej rýchlosť, alebo mení smer rýchlosti. Ak pohybujúca sa častica zmenila svoju rýchlosť vzhľadom k zvolenej inerciálnej sústave, musela byť vykonaná práca iným telesom. Hovoríme, že práca na častici bola vykonaná inou silou, výsledkom ktorej je zmena pohybu častice. Dynamická veličina, ktorá súvisí s pohybom a ktorá sa v dôsledku vykonania práce zmenila sa nazýva kinetickou energiou.
Uvážime prípad, keď pôsobiaca sila f má smer rýchlosti častice. Vtedy aj zrýchlenie a, ktoré sila častici udelí, má smer rýchlosti. Preto aj elementárna zmena rýchlosti dv je rovnobežná s vektorom rýchlosti, takže pre skalárny súčin v . dv platí rovnosť v . dv = v dv.
![]()
Potom môžeme písať
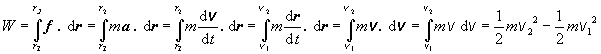 (2.2.5.2)
(2.2.5.2)Súčasne, podľa vzorca (2.2.5.1), platí W = E2 - E1 , takže porovnaním získame vzťah pre kinetickú (pohybovú) energiu :
Rovnicu (2.2.5.2) s využitím vzťahu (2.2.5.3) možno prepísať do tvaru:
ktorá má názov „ veta o kinetickej energii pre hmotný bod“ , alebo teoréma práce. Vzťah (2.2.5.4) hovorí:
Zmena kinetickej energie hmotného bodu sa rovná práci vykonanej výslednicou pôsobiacich síl pri premiestnení hmotného bodu z počiatočnej polohy do konečnej polohy.
Táto veta sa často využíva pri riešení príkladov, kedy máme určiť rýchlosť bodu v určitom mieste trajektórie, alebo keď rýchlosť v určitom bode je známe a máme určiť iný parameter trajektórie. Súvislosť medzi kinetickou energiou a hybnosťou v klasickej newtonovskej mechanike určuje rovnica
kde p1, resp. p2 je veľkosť počiatočnej a konečnej hybnosti hmotného bodu .
Jednotkou kinetickej energie v sústave SI je rovnako ako pre prácu 1 J = 1 N.m = 1 kg. m2. s-2
Vychádzajúc z porovnania vzorcov by sme vlastne mali vo vzťahu (2.2.5.3) písať Ek = (1/2)mv2 + C , kde C je ľubovoľná konštanta, ktorá sa pri odčítaní hodnôt Ek2 - Ek1 vynuluje. Jej ponechanie vo vzorci by však znamenalo, že vo vzťažnej sústave, v ktorej je častica v pokoji (v = 0) by častica mala nenulovú kinetickú energiu. Preto sa pre kinetickú energiu častice akceptuje vzorec (2.2.5.3) . Treba však podotknúť, že vzhľadom na inú vzťažnú sústavu, ktorá sa vzhľadom na prvú pohybuje, kinetická energia tej istej častice nie je nulová.
Poznámka
Postup pri odvodzovaní (2.2.5.2) možno naznačiť pomocou diferencií :
DW = f Dr = ma Dr = m (Dv /Dt) Dr = m (Dr /Dt) Dv = m v Dv
Poznámka
Skalárny súčin v dv , vystupujúci vo vzťahu (2.2.5.2) sa vždy rovná výrazu v dv , bez ohľadu na to, či vektory v a dv sú rovnobežné. To možno ukázať dvomi postupmi.
a) Diferencovaním výrazu (v v)
d(v v) = dv v + v dv = 2 v dv
alebo inak,
d(v v) = d(v v cos 0) = d(v2 ) = 2 v dv
Z porovnania výsledkov ihneď vyplynie rovnosť v d v = v dv
b) Vyjadrením vektora v a jeho diferenciálu pomocou jednotkového vektora
v = v t , dv = d(vt )
Treba si pritom uvedomiť, že jednotkový vektor nemôže meniť svoju veľkosť, iba smer, preto jeho elementárna zmena dt je vektor kolmý na vektor t , takže ich skalárny súčin ( t dt ) sa rovná nule . Preto platí :
v dv = (v t ) d(vt ) = (v t ) (dv t + v dt ) = v dv ( t t ) + v2 ( t dt ) = v dv
Príklad 2.2.5.1
Akú prácu treba vykonať na zvýšenie rýchlosti automobilu z 36 km/h na 72 km/h ? Za aký časový interval to možno dosiahnuť, ak motor automobilu má výkon 50 kW ? Hmotnosť automobilu m = 1200 kg.
Riešenie
Potrebnú prácu vypočítame ako rozdiel kinetických energií
Pre porovnanie si všimnime, že pôvodná kinetická energia auta bola 600 kg 102 m2s-2 = 60 000 J. Ak má motor výkon P = 50 000 W, prácu W = 180 000 Ws vykoná za časový interval
Dt = W / P = 3,6 s
Reálne to však trvá dlhšie, lebo značná časť práce vykonanej motorom sa vynaloží na prekonávanie odporu prostredia.
B) Potenciálna energia
Súvisí s polohou častice vo vzťažnej sústave, preto sa pre ňu používa aj názov polohová energia. Ide o polohu vzhľadom na iné teleso (alebo časticu), pričom medzi časticou a telesom existuje vzájomné silové pôsobenie. Hovoríme, že častica sa nachádza v silovom poli (telesa), čo znamená, že v každom bode silového poľa na časticu pôsobí určitá sila, ktorej veľkosť aj smer sa s polohou častice môže meniť. Najjednoduchším prípadom je homogénne silové pole, v ktorom veľkosť aj smer sily sú v každom bode poľa rovnaké. V istom priblížení takýmto poľom je gravitačné pole Zeme, ak sa obmedzíme na oblasť blízko zemského povrchu.
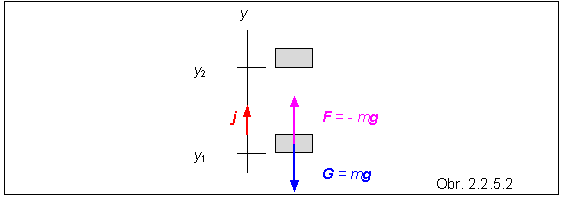
V takomto poli budeme dvíhať teleso s hmotnosťou m z východiskovej polohy, ktorej zodpovedá výšková súradnica y1 do konečnej polohy so súradnicou y2 . Tiaž G telesa ako vektorová veličina smeruje nadol, proti jednotkovému vektoru j zatiaľ čo sila F, ktorou dvíhame teleso (bez zrýchlenia !), má rovnakú veľkosť, ale smeruje nahor. Prácu na zodvihnutie telesa vypočítame integrálom
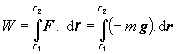
Do integrálu dosadíme g = - g j , dr = j dy , a integračné medze zameníme na y1 a y2:
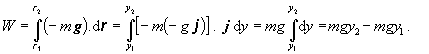 (2.2.5.6)
(2.2.5.6)Vykonaná práca sa rovná rozdielu hodnôt potenciálnej energie telesa v dvoch polohách, preto za potenciálnu energiu v tomto prípade považujeme výraz
Ep = mgy (2.2.5.7)
Aj v tomto prípade, podobne ako pri kinetickej energii, možno k výrazu mgy pripočítať ľubovoľnú konštantu. Ak vo zvolenej vzťažnej sústave považujeme potenciálnu energiu za nulovú vtedy, keď výšková súradnica častice je nulová, potom aj konštanta sa rovná nule.
Poznámka
Potenciálna energia, na rozdiel od kinetickej, môže mať v niektorých polohách zápornú hodnotu. Ak napríklad potenciálnu energiu závažia položeného na stole budeme považovať za nulovú, potom na dlážke miestnosti bude jeho potenciálna energia záporná. Poloha nulovej hladiny potenciálnej energie závisí od našej voľby.
Pri odvodzovaní vzťahu (2.2.5.4) bola použitá sila F , pôsobiaca nahor, proti tiaži telesa. Tiaž telesa môžeme chápať ako silu f , ktorou silové (tiažové) pole pôsobí na časticu (teleso) . Sily F a f sú rovnako veľké, ale majú opačný smer : f = - F . Ak kladná práca sily F zvýši potenciálnu energiu častice, potom kladná práca sily f potenciálnu energiu častice zmenší. Preto ak časticu posúvajú sily poľa, konajú prácu na úkor potenciálnej energie častice. Pre elementárnu prácu to môžeme zapísať v tvare
f . dr = - dEp (2.2.5.8)
Pritom
f . dr = (fx i + fy j + fz k ) . (i dx + j dy + k dz) = fx dx + fy dy + fz dz
Pri odvodzovaní vzťahu (2.2.5.4) sme uvažovali o sile, ktorá má zložku len v smere osi y a v tomto smere sme teleso aj posúvali, preto v tomto prípade možno napísať rovnosť f . dr = fy dy , takže platí
fy dy = - dEp (2.2.5.9)
Po integrácii rovnice (2.2.5.9) dostaneme vzťah
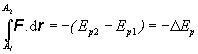 (2.2.5.10)
(2.2.5.10)ktorý možno interpretovať: „Práca konzervatívnych síl nezávisí od trajektórie. V konzervatívnom systéme definujeme veličinu potenciálnej energie Ep “. Je vhodné si uvedomiť:
„Práca vykonaná v konzervatívnom systéme sa rovná úbytku potenciálnej energie systému Ep,.“
V prípade kinetickej energie sme zistili, že práca výslednej sily sa rovná prírastku kinetickej energie (rovnica (2.2.5.4)).
Zo vzorca (2.2.5.9) vyplýva veľmi významný vzťah používaný v teórii polí
V trojrozmernom priestore , keď pôsobiaca sila poľa nemá smer niektorej súradnicovej osi, pribudnú aj členy
takže celú silu vyjadrujeme v tvare
Vo výslednom vzorci, tak ako to má byť, vystupujú parciálne derivácie potenciálnej energie, čo znamená, že napr. pri derivovaní v smere osi x , zvyšné dve súradnice považujeme za nemenné - všímame si zmenu potenciálnej energie len v smere jednej osi.
Podrobnosti o výraze typu (2.2.5.12) možno nájsť v kapitole o vektorovom počte, v časti o deriváciách vektorových funkcií, pod názvom gradient skalárnej funkcie.
C) Energia stlačenej pružiny
Stlačená pružina je zdrojom mechanickej energie, ktorá sa využíva napríklad v mechanických hodinkách či hračkách. Vypočítame, koľko energie možno uskladniť v pružine pri jej stlačení. Čím väčšie je stlačenie pružiny x (jej skrátenie), tým väčšou silou f je potrebné na pružinu pôsobiť. Preto medzi týmito veličinami platí vzťah f = kx . Elementárnu prácu tejto sily vyjadríme pomocou jednotkového vektora j (podľa obrázku) :
f . dr = ( f j ) .d( x j ) = f dx = kx dx.
Integráciou získame vykonanú prácu :
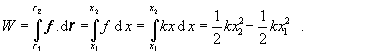 (2.2.5.13)
(2.2.5.13)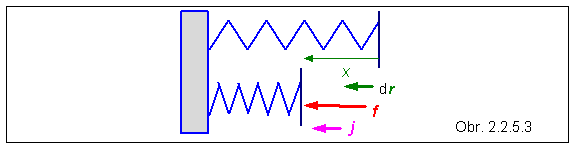
Výsledok ukazuje, že práca vonkajšej sily má za následok zmenu veličiny kx2/2 , ktorú považujeme za energiu stlačenej pružiny. Túto energiu v podstate možno považovať za iný druh potenciálnej energie, lebo vo výslednom vzorci nevystupuje rýchlosť, ale výsledná poloha (skrátenie, resp. predĺženie) pružiny.
Príklad 2.2.5.2
Drôtenú špirálu dĺžky l0 predĺžime silou F1 o dĺžku D x. Aká práca sa vykoná pri predĺžení špirály na trojnásobok jej pôvodnej dĺžky, keď sila konajúca prácu pôsobí v smere predĺženia a je úmerná predĺženiu špirály?
Riešenie
Pôsobiaca sila nie je konštantná, je funkciou predĺženia F = kx. Prácu premennej sily vypočítame na základe vzťahu (2.2.4.1), v ktorom zvážime, že elementárne posunutie sa uskutočňuje v jednom smere zhodnom so smerom pôsobiacej sily (zvolili sme os x). Zmena na trojnásobok pôvodnej dĺžky odpovedá práci pri predĺžení v hraniciach <0, 2l0>
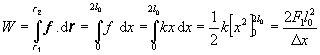
kde sme konštantu k vyjadrili podielom F1/D x.
Kontrolné otázky
-
Ktorá veličina nám charakterizuje pohybový, alebo polohový stav mechanickej sústavy?
-
Aké jednotky v sústave SI sa používajú pre prácu a energiu?
-
Vyjadrite jednotku 1 J pomocou základných jednotiek sústavy SI.
-
Definujte pojem kinetická energia a napíšte jej matematické vyjadrenie. Uveďte význam v nej vystupujúcich veličín.
-
Definujte pojem potenciálna energia a napíšte jej matematické vyjadrenie. Uveďte význam v nej vystupujúcich veličín.
-
Napíšte ako súvisí práca s kinetickou energiou.
-
Napíšte ako súvisí práca s potenciálnou energiou.
-
Uveďte niektoré špeciálne prípady mechanickej energie.
-
Vyslovte vetu o kinetickej energii.
-
Napíšte vzťah určujúci súvislosť medzi pôsobiacou silou a potenciálnou energiou.
-
Vyjadrite prácu stlačenej pružiny.
