 Zákony zachovania, pohybové rovnice
Zákony zachovania, pohybové rovnice
V nasledujúcej časti urobíme porovnania najvšeobecnejších fyzikálnych zákonov. Jedným zo základných princípov fyziky a prírodných vied je kozmologický princíp: - fyzikálne deje prebiehajú nezávisle od voľby miesta v časopriestore (-štvorrozmerný priestor, so štvrtým rozmerom vyjadrujúcim plynutie času). Rovnako základnými princípmi sú i zákony zachovania. Zákony zachovania fyzikálnych veličín v izolovanej sústave, ako sú zákon zachovania hybnosti, zákon zachovania energie sa vyznačujú spomedzi iných fyzikálnych zákonov predovšetkým svojou všeobecnosťou. Zákony zachovania i kozmologický princíp sa uplatňujú v klasickej i kvantovej, nerelativistickej i relativistickej fyzike, v rozmeroch mikročastíc i galaxií. Boli objavené na základe pokusov ako zovšeobecnenie mnohých pozorovaní i experimentálnych faktov.
Až neskôr bol objavený ich vzájomný súvis umožňujúci vysvetliť ich všeobecnosť, ale aj dať podmienky, za ktorých ich platnosť môže byť narušená. Zákony zachovania priamo súvisia so vzťažnou sústavou, vlastnosťami časopriestoru. Konkrétne ide o skutočnosť nepremennosti fyzikálnych zákonov - ich invariantnosti pri určitých transformáciách. Treba upozorniť, že nám ide o vlastnosti zákonov, nie predmetov, nie o symetriu kryštálu, tvar galaxie. Invariantnosťou sme vyjadrili napr. zákon, že všetky fyzikálne sústavy sú ekvivalentné, fyzikálne zákony v nich nadobúdajú rovnaký tvar. Pritom jednotlivé fyzikálne veličiny sú relatívne, transformujú sa pri zámene vzťažnej sústavy. Pri skúmaní jednotlivých typov symetrie sa ukazuje súvis s konkrétnym zákonom zachovania.
Translačná symetria priamo súvisí so zákonom zachovania hybnosti. Translačná symetria vyjadruje skutočnosť, že priestor je homogénny. Dej prebiehajúci v jednom mieste vesmíru, bude prebiehať rovnako i v inej časti vesmíru, samozrejme za predpokladu presunu všetkých pre dej podstatných skutočností (experiment môžem zopakovať v inom laboratóriu s rovnakým výsledkom).
Symetria vzhľadom na posunutie v čase priamo súvisí so zákonom zachovania energie. Táto symetria vyjadruje skutočnosť, že fyzikálne zákony sa plynutím času nemenia. V rôznom čase začínajúce rovnaké časové intervaly sú ekvivalentné v tom zmysle, že fyzikálny dej prebiehajúci za rovnakých podmienok bude prebiehať rovnako, nezávisle na okamihu jeho začiatku.
Rotačná symetria priestoru priamo súvisí so zákonom zachovania momentu hybnosti. Vyjadruje skutočnosť, že pootočenie experimentu, voľbou orientácie súradnicovej sústavy nerozhoduje o priebehu deja. Treba si uvedomiť, že ide o otočenie každej s javom súvisiacej príčiny. (Voda z nakolnenej vaničky sa nevyleje len v tom prípade, ak otočíme rovnako i tiažové pole.).
Symetria voči Lorentzovej (v newtonovskej mechanike Galileiho transformácii) priamo súvisí so zákonom zachovania pohybového stavu hmotného stredu. V Lorentzovej transformácii s ním priamo súvisí i transformácia hybnosti a skladanie hmotností. Problém naznačíme v kapitole o teórii relativity.
V mechanike sústavy hmotných bodov sme odvodili prvú pohybovú rovnicu sústavy hmotných bodov. Plynie zo zákona zachovania hybnosti v izolovanej sústave.
Definujeme postupne nové fyzikálne veličiny, ukážeme ich význam a naznačíme postup všeobecného odvodenia.
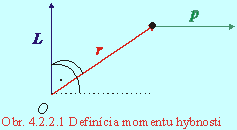
Moment hybnosti častice L vzhľadom na daný vzťažný bod O je vektorová veličina daná vektorovým súčinom polohového vektora r častice a hybnosti častice p (Obr. 4.2.2.1).
Moment hybnosti častice závisí od voľby vzťažného bodu. Preto: moment hybnosti je vektor umiestnený do vzťažného bodu O:
Na základe doteraz odvodených rovníc pre hmotný bod a sústavu hmotných bodov a rotačnej symetrie vzťažnej sústavy odvodíme teraz pre tuhé teleso druhú pohybovú rovnicu a zákon zachovania momentu hybnosti. Vyjdime z druhej pohybovej rovnice a zákona zachovania momentu hybnosti pre sústavu hmotných bodov. Formálne sa zdá, že druhá pohybová rovnica vznikne z prvej len vektorovým prenásobením polohovým vektorom a obe tieto rovnice by nemali byť nezávislé. V skutočnosti prenásobením sily vektorov polohovým vektorom vzhľadom na zvolený vzťažný bod dostávame moment sily, čo je iná fyzikálna veličina ako sila.
Prejdime v mechanike tuhého telesa od sústavy hmotných bodov k telesu so spojito rozloženou hmotnosťou.
Teleso si môžeme predstaviť ako sústavu nekonečného počtu častí, ktoré spojito vyplňujú objem telesa. Objem každej časti telesa je elementárny objem dt = dx dy dz a jeho hmotnosť je daná súčinom hustoty (objemovej hmotnosti) v danom mieste telesa r(x,y,z) a elementu objemu dt, dm = r dt . Pohybové rovnice sústavy častíc sú pohybové rovnice aj pre dokonale tuhé teleso, s tým rozdielom, že v definíciách veličín vystupujúcich v týchto rovniciach je sumácia nahradená integrálom. Stručne ich zhrňme:
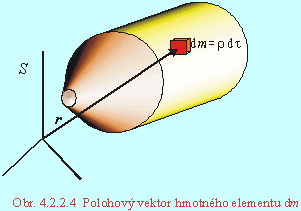
Hmotnosť telesa m :
Hmotný stred:
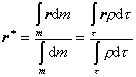
kde r je polohový vektor hmotného elementu dm (Význam veličín vyplýva z Obr.4.2.2.4.)
Hybnosť telesa:
kde v je rýchlosť hmotného elementu dm.
Hybnosť hmotného stredu:
je rýchlosť hmotného stredu.
Moment hybnosti tuhého telesa:
vzťažný bod je začiatok polohového vektora r, ktorý určuje polohu hmotného elementu dm pohybujúceho sa rýchlosťou v.
Pre takto definované veličiny charakterizujúce tuhé teleso, platia rovnaké rovnice, ako pre pohyb sústavy častíc.
Prvá pohybová rovnica pre dokonale tuhé teleso:
časová zmena celkovej hybnosti tuhého telesa sa rovná výslednici vonkajších síl.
Veta o pohybe hmotného stredu (ťažiska):
časová zmena hybnosti hmotného stredu sa rovná výslednici vonkajších síl, hmotný stred sa pohybuje tak, ako keby v ňom bola sústredená celá hmotnosť a pôsobila naň výslednica vonkajších síl.
Druhá pohybová rovnica pre dokonale tuhé teleso:
časová zmena celkového momentu hybnosti sa rovná výslednici momentu vonkajších síl vzhľadom na ten istý momentový bod.
Integráciou cez časový interval dostávame tzv. impulzové vety.
Prvá impulzová veta:
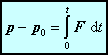 (4.2.2.9)
(4.2.2.9)kde p, p0 sú celkové hybnosti telesa na konci resp. začiatku časového intervalu.
Druhá impulzová veta:
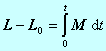 (4.2.2.10)
(4.2.2.10)kde L a Lo sú celkové momenty hybnosti telesa na konci resp. začiatku časového intervalu.
Základnými rovnicami sú pohybové rovnice. Impulzové vety majú význam hlavne pre úlohy, kde sila (moment sily) pôsobí len počas daného časového intervalu, t. j. pred týmto intervalom je hybnosť (moment hybnosti) konštantná a konečná hodnota po skončení vonkajšieho pôsobenia sa ďalej nemení.
