 Vzťah medzi elektrickou a tepelnou vodivosťou v kove
Vzťah medzi elektrickou a tepelnou vodivosťou v kove
Zo skúsenosti vieme, že materiály, ktoré majú veľmi nízku elektrickú vodivosť (izolanty) majú aj nízku tepelnú vodivosť. V týchto látkach niet voľných nábojov a tak odovzdávanie kinetickej energie pri tepelných kmitoch ide len od jednej častice v uzle kryštalickej mriežky k druhej. Podľa malej tepelnej vodivosti môžeme usúdiť, že takýto prenos tepla je málo výkonný. Kovy sú tisíckykrát tepelne vodivejšie ako izolanty. Z toho usudzujeme, že v kovoch musí byť ešte iný, oveľa výkonnejší mechanizmus prenosu tepla. Na rozdiel od izolantov, v kove sú voľné elektróny a tepelná vodivosť elektrónového plynu v kove bude teda určujúca pre prenos tepla kovom. Takže bez veľkej chyby môžeme použiť vzťah odvodený pre koeficient mernej tepelnej vodivosti ideálneho plynu
![]()
kde k je Boltzmannova konštanta, n je koncentrácia (v našom prípade) elektrónového plynu, ostatné veličiny boli vysvetlené v predošlej časti. Vypočítajme pomer k/s
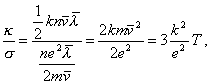 (9.3.1)
(9.3.1)
kde sme použili vzťah
![]() .
.
Z tohoto výsledku vidíme, že pri danej teplote pomer k/s nezávisí od druhu kovu, je pre všetky kovy rovnaký. Tento zákon sa nazýva zákon Wiedemanna - Franza, ktorí ho získali z výsledkov meraní.
Pri teplote T0 nech sú hodnoty merných vodivostí k0 a s0 a pri teplote T = T0 + DT nech sú tieto hodnoty k a s. Zo vzťahu (9.3.1) vyplýva
![]()
odkiaľ
![]()
Ak si zvolíme T0 = 273 K, potom bude a = 1/273 = 3,67.10-3 K-1. Pokusy s meraním koeficientu a pre rôzne kovy ukázali dobrú zhodu s touto hodnotou.
Keďže experiment ukázal, že koeficient mernej tepelnej vodivosti kovov od teploty nezávisí, bude k = k0 a z poslednej rovnice vyplynie
![]() (9.3.2)
(9.3.2)
čo je vzťah pre teplotnú závislosť merného odporu.
Príklad 9.3.2: K zdroju je pripojený odizolovaný drôt, ktorý sa prechodom prúdu zohreje na určitú teplotu. Potom začneme jednu polovicu drôtu ofukovať. Ako sa zmení teplota druhej polovice drôtu?
Riešenie Ofukovaná (t.j. chladená) polovica drôtu zníži svoj odpor, rozdelenie napätí sa zmení: väčšie napätie teraz bude na neofukovanej polovici. Teplo vytvorené na tejto polovici je úmerné (Uneofukovanej.polovice)2, čo znamená, že teplota neofukovanej polovice sa zvýši. To ale vedie k novému prerozdeleniu napätia medzi polovicami, už opísaným mechanizmom sa ešte viac zvýši teplota neofukovanej polovice, atď. Nakoniec sa ustáli rovnovážny stav.
Kontrolné otázky
- Rezistor pri teplote T0 má odpor R0. Aký bude jeho odpor pri teplote T? Rezistivitu jeho materiálu poznáme.
- Ako vysvetlíte, že odpor kovového rezistora s teplotou rastie?
- Ako by ste prepísali vzťah (9.3.2) pre konduktivitu?
- Prečo majú kovy dobrú elektrickú aj tepelnú vodivosť?
