Ak v elektrickej sieti vykonáme nejakú zmenu, napr. pripojíme zdroj, zmeníme hodnotu rezistora, prepínačom zmeníme konfiguráciu siete a podobne, prúdy a napätia vo vetvách siete sa prispôsobia týmto zmenám. Ak sieť obsahuje kondenzátory a cievky, ktoré viažu energiu elektrického, alebo magnetického poľa, toto prispôsobovanie trvá určitý čas. Javy, ktoré v sieti pri tom prebiehajú, nazývame prechodovými javmi. V tomto paragrafe ukážeme ako sa správajú napätia a prúdy v jednoduchej sieti s jednosmerným zdrojom, rezistorom a kondenzátorom.

 

1. Vybíjanie kondenzátora

Vezmime si elektrickú sieť, v ktorej bude zdroj jednosmerného napätia U, vypínač, kondenzátor s kapacitou C a rezistor s odporom R podľa obr. 9.9.1. V čase t = 0 odpojíme zdroj. Ostane len do série zapojený kondenzátor s rezistorom a nastane vybíjanie kondenzátora cez rezistor.

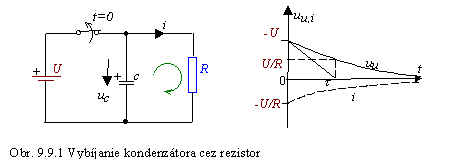
Napíšeme rovnicu podľa 2. Kirchhoffovho zákona:

(a)

kde prvý člen je napätie na rezistore a druhý člen je napätie na kondenzátore. Prúd tečie vďaka úbytku náboja q na kondenzátore, t.j. i = -dq/dt , u_C = -q/C, čo dosadíme do (a) a rovnicu upravíme

odkiaľ

Integrovaním dostaneme

odkiaľ

Konštantu k nájdeme z počiatočnej podmienky q₀ = CU v čase t = 0. Vyjde nám CU = k a posledná rovnica nadobudne tvar

(b)

Z náboja môžeme získať napätie na kondenzátore a prúd:

(9.9.1)

(d)

Vidíme, náboj sa postupne mení od počiatočnej hodnoty q₀ postupne k nule. Nemôže sa zmeniť skokom, lebo na prenos náboja treba vykonať prácu a práca sa nedá vykonať za nulový čas (na to by sme potrebovali zariadenie s nekonečne veľkým výkonom). Grafy časových závislostí napätia na kondenzátore a prúdu sú na obr. 9.9.1. Ani napätie na kondenzátore sa nemení skokom. Energia elektrického poľa v kondenzátore je W_e = CU²/2 a ako vieme, energia sa môže zmeniť len prácou, a teda z rovnakých dôvodov nemôže byť zmenená skokom.

 

2. nabíjanie kondenzátora

V elektrickom obvode pozostávajúcom zo zdroja, vypínača, rezistora s odporom R a kondenzátora s kapacitou C (všetky prvky sú zapojené sériovo, obr. 9.9.2) v čase t = 0 zapneme vypínač. Obvod bude uzavretou slučkou a môžeme napísať 2. Kirchhoffov zákon:

Prúd je spôsobený prirastaním náboja na kondenzátore, t.j. i = dq/dt a u_C = q/C. Po dosadení a úprave

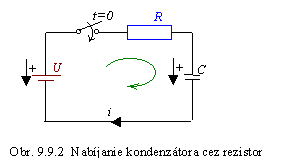
Riešenie homogénnej diferenciálnej rovnice (bez pravej strany) je

Celkové riešenie navrhneme také, aby spĺňalo počiatočnú podmienku . Riešenie bude

Ak do tejto rovnice dosadíme t =0 , dostaneme k = -CU. Takže riešenie bude

(e)

Odtiaľto získame

(9.9.2)

(f)

Grafy závislostí (e), (9.9.2), (f) sú na obr. 9.9.3.

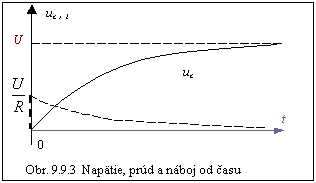
Príklad 9.9.1: Máme k dispozícii zdroj s napätím U, kondenzátor so známou kapacitou C, voltmeter s vysokým (ale konečným) vnútorným odporom R_V, neznámy rezistor s vysokou hodnotou R_x a stopky. Navrhnite spôsob ako by ste meraním určili R_x .

Riešenie  Môžeme použiť vybíjanie kondenzátora (odpojeného od zdroja) cez neznámy rezistor a merať časovú závislosť poklesu napätia na kondenzátore. Súčiastky a zdroj zapojíme podľa obr. 9.9.1 a navyše pripojíme voltmeter ku kondenzátoru. Napätie na kondenzátore udáva rovnica (9.9.1), kde v tomto prípade R je paralelné zapojenie R_V a R_x ,lebo kondenzátor sa vybíja aj cez voltmeter:

Potom odpojíme neznámy rezistor, kondenzátor znovu nabijeme, zdroj odpojíme a kondenzátor necháme vybíjať cez voltmeter:

Z merania času a napätia dostaneme experimentálne body uvedených závislostí u_C1 a u_C2. Zlogaritmovaním rovníc pre napätia a nakreslením grafov ln u_C1(t) a ln u_C2(t) , kde

môžeme nájsť zo smerníc týchto priamok hodnoty R_V a R_Vx, z ktorých vypočítame R_x.

Príklad 9.9.2: Máme nabitý kondenzátor na napätie U, ktorý necháme vybiť cez rezistor R. Koľko tepla Q sa vytvorí v rezistore?

Riešenie  Za čas dt sa vytvorí v rezistore teplo dQ = R i² dt . Veľkosť vybíjacieho prúdu je daná podľa vzťahu (d), takže dQ bude

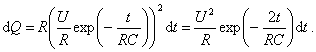
Integrovaním tohto výrazu od 0 do ¥ dostaneme množstvo tepla vytvoreného v rezistore počas vybíjania kondenzátora

čo je počiatočná energia elektrického poľa v kondenzátore.

Kontrolné otázky

1. Na nabitie kondenzátora treba vynaložiť prácu. Môže byť kondenzátor nabitý za nulový čas?
2. Relaxačným časom nazývame čas, pri ktorom napätie na kondenzátore (pri jeho vybíjaní) sa zmenší e krát. Čomu sa rovná tento čas? Použite (9.9.1).
3. Môžeme povedať, že relaxačný čas charakterizuje schopnosť RC obvodu prísť do nového rovnovážneho stavu po manipulácii s vypínačom?
4. Prečo sa prúd v prípadoch 1 a 2 mohol zmeniť v čase t = 0 skokom, ale napätie nie?