 Magnetický tok
Magnetický tok
Magnetický tok F je integrál magnetickej indukcie B cez orientovanú plochu S
![]() (10.5.1.1)
(10.5.1.1)
Analogickým vzťahom je definovaný elektrický prúd I cez hustotu elektrického prúdu j, preto je vlastne magnetická indukcia B hustotou magnetického toku F. Jednotka magnetického toku v sústave SI weber (Wb) je pomenovaná podľa nemeckého fyzika Wilhelma Eduarda Webera (1804-1891). Zrejme 1 Wb = 1 T.m2. Ak je magnetická indukcia B v každom bode povrchu S rovnaká a súhlasne orientovaná s vektorom dS (slučka l leží v rovine kolmej na homogénne magnetické pole), získame
![]() (10.5.1.2)
(10.5.1.2)
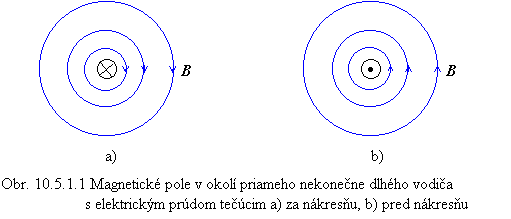
V časti 10.4.1 a v príklade 10.4.1.1 sa konštatuje, že v okolí nekonečne dlhého priameho prúdovodiča sa vytvorí magnetické pole, v ktorom sa smer magnetickej indukcie B určuje zahnutými prstami podľa pravidla pravej ruky, takže magnetické indukčné čiary sú orientované koncentrické kružnice ležiace v rovinách kolmých na prúdovodič, pozri obr. 10.5.1.1. V experimentoch bol tento jav pozorovaný dánskym fyzikom Hansom Christianom Oerstedom (1777-1851).
Zdrojom magnetického poľa s uzavretými magnetickými indukčnými čiarami je tiež cievka s elektrickým prúdom, pozri obr. 10.5.1.2a. Mechanickým lámaním tyčového permanentného magnetu sa nepodarí izolovať severný pól od južného pólu, nevytvoria sa magnetické monopóly, ktoré by mohli samostatne existovať. Každý zlomok tyčového magnetu je nový magnet so svojím severným a južným pólom (je magnetickým dipólom). To ale znamená, že magnetické indukčné čiary nezačínajú v severnom a nekončia v južnom póle trvalého magnetu, ale sú uzavreté a vychádzajú zo severného a vchádzajú do južného pólu permanentného magnetu, pozri obr. 10.5.1.2b.
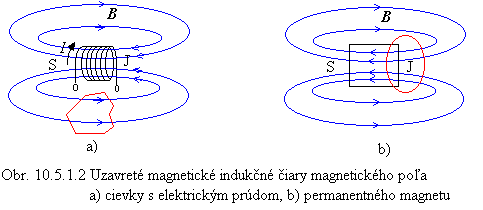
Magnetické indukčné čiary vnútri trvalého magnetu sú pokračovaním magnetických indukčných čiar v okolí magnetu, podobne ako vnútri cievky (solenoidu) s elektrickým prúdom. Magnetické polia trvalých magnetov sú vyvolané interakciou spinov elektrónov susedných atómov v doméne a nevratnosťou zmeny orientácie magnetických momentov domén v magnetizačných procesoch. Keďže sú magnetické indukčné čiary uzavreté, musí ich vychádzať z ľubovoľného uzavretého (Gaussovho) povrchu práve toľko, koľko ich do neho vchádza. Červené krivky na obr. 10.5.1.2 sú rezy uzavretých Gaussových povrchov rovinou nákresne. Nemecký matematik, fyzik a astronóm Karl Friedrich Gauss (1777-1855) sformuloval zákon známy pod názvom Gaussova veta pre magnetický tok: magnetický tok cez ľubovoľný uzavretý povrch S sa vždy rovná nule
![]() (10.5.1.3)
(10.5.1.3)
Vektor dS plošného obsahu dS elementu uzavretého povrchu vo vzťahu (10.5.1.3) je podľa konvencie kolmý na element povrchu, jeho smer je von z objemu V ohraničeného uzavretým povrchom S. Zo vzťahu (10.5.1.3) nevyplýva nulovosť magnetickej indukcie B, pretože povrch S je uzavretým topologickým objektom. Ak na ľavú stranu aplikujeme vetu Ostrogradského-Gaussa, dostaneme
![]()
Integrál po „otvorenom“ objeme V ohraničenom uzavretým povrchom S je nulový, ak sa nule rovná podintegrálna funkcia. Z posledného vzťahu vyplýva diferenciálna rovnica, ktorá platí pre stacionárne i nestacionárne magnetické polia. Formuloval ju anglický fyzik James Clerk Maxwell (1831-1879) a zvyčajne sa označuje ako 3. Maxwellova rovnica
![]() (10.5.1.4)
(10.5.1.4)
Rovnica vyjadruje to, že magnetické indukčné čiary nemajú začiatok (žriedlo, prameň) a nemajú koniec (prepad, ústie). Magnetické pole je totiž nežriedlové, na rozdiel od elektrického poľa, v ktorom elektrické indukčné čiary začínajú na kladných elektrických nábojoch a končia na záporných elektrických nábojoch. Kladný elektrický náboj je žriedlom elektrických indukčných čiar, záporný náboj je prepadom elektrických indukčných čiar.
Aplikujme na ľavú stranu Ampérovho zákona (10.4.2.10) Stokesovu vetu. Vodivostný (kondukčný) elektrický prúd I a Maxwellov posuvný prúd Ip vyjadrime integrálmi po ploche S ohraničenej orientovanou uzavretou krivkou l. Úpravou získame
![]()
kde j je hustota kondukčného elektrického prúdu I , D je elektrická indukcia v bodoch plochy S. Porovnanie podintegrálnych funkcií vedie k diferenciálnej rovnici, ktorá platí pre stacionárne i nestacionárne magnetické polia. Zvyčajne sa označuje ako 4. Maxwellova rovnica
![]() (10.5.1.5)
(10.5.1.5)
V časti (10.1.2) sa konštatuje, že stacionárne magnetické (magnetostatické) pole je vyvolané stacionárnym prúdovým poľom. Také prúdové pole nemôže byť zdrojom nestacionárnych elektrických polí, preto má 4. Maxwellova rovnica pre magnetostatické pole tvar
![]() (10.5.1.6)
(10.5.1.6)
Príklad 10.5.1.1
Gaussov uzavretý povrch má tvar povrchu valca s polomerom podstáv 10 cm a s výškou 80 cm. Vypočítajte magnetický tok cez plášť valca, ak magnetický tok cez spodnú podstavu je 20 mWb a vrchná podstava sa nachádza v homogénnom magnetickom poli s magnetickou indukciou B veľkosti 10 T orientovanou kolmo na podstavu do valca.
Riešenie
Označme polomer podstáv R = 10 cm = 0,1 m. Označme magnetický tok cez spodnú podstavu F1 = 20 mWb. Keďže je tento tok kladný, vychádza cez spodnú podstavu z valca von. Vypočítame magnetický tok F2 cez vrchnú podstavu
![]()
Keďže je magnetický tok F2 záporný, vchádza cez vrchnú podstavu do valca. Podľa Gaussovej vety (10.5.1.3) sa magnetický tok cez uzavretú plochu rovná nule, preto
![]()
Po úprave a dosadení pre magnetický tok F3 cez plášť valca dostaneme
![]()
Magnetický tok F3 = 294 mWb je kladný, preto vychádza cez plášť valca z valca von.
