 Vlastná a vzájomná indukčnosť
Vlastná a vzájomná indukčnosť
Magnetický tok F cez plochu ohraničenú závitom (uzavretým vodičom, napr. aj cievkou) môže byť vyvolaný permanentným magnetom nachádzajúcim sa v blízkosti závitu, ale aj elektrickým prúdom prechádzajúcim buď samotným závitom, alebo vodičom nachádzajúcim sa v jeho blízkosti. Ak je magnetický tok F budený elektrickým prúdom I , potom sa ukazuje, že je priamoúmerný pretekajúcemu prúdu :

Ak je magnetický tok budený prúdom tečúcim cez ten istý uzavretý vodič (závit), potom L je vlastná indukčnosť, ak prúdom tečúcim cez iný vodič, ide o vzájomnú indukčnosť.
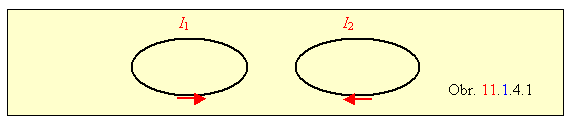
Uvážime tieto dva prípady - podľa obrázku, kde pre jednoduchosť sú dva uzavreté vodiče nakreslené ako dva závity. Prvým závitom tečie prúd I1 , druhým I2 .
Magnetický tok je definovaný integrálom
![]()
pričom vektor magnetickej indukcie B sa počíta podľa Biotovho - Savartovho zákona. Pre vektor B1 v okolí prvého vodiča preto platí
![]()
Spojením dvoch predošlých vzorcov dostaneme pre magnetický tok F21 plochou ohraničenou druhým závitom, ale vyvolaným prúdom tečúcim prvým závitom :
![]() (11.1.4.2)
(11.1.4.2)
kde L21 , vyjadrený ako plošný integrál, je vzájomná indukčnosť. Podobným postupom možno získať vzťah pre vlastnú indukčnosť, ak namiesto integrácie cez plochu ohraničenú druhým vodičom, sa integruje vektor B1 cez plochu ohraničenú prvým vodičom.
Vychádzajúc zo vzťahu (11.1.4.1) a z Faradayovho zákona, pre indukované elektromotorické napätie, dostaneme všeobecný vzorec (bez ohľadu na to, či ide o vlastnú, alebo vzájomnú indukčnosť) :

Poznámka Ak je indukčný tok budený prúdom tečúcim jednak samotným vodičom, jednak vodičom susedným, vzorec 11.1.4.3 bude pozostávať z dvoch členov - člena ktorý obsahuje vlastnú indukčnosť a člena obsahujúceho vzájomnú indukčnosť:
![]()
Jednotkou vlastnej i vzájomnej indukčnosti je henry (H) . Vlastnú indukčnosť veľkosti 1 H má cievka, v ktorej sa pri zmene elektrického prúdu o 1 A za 1 s indukuje na koncoch elektrické napätie 1 V .
Príklad 11.1.4.1 Vypočítajte vlastnú indukčnosť tenkej toroidálnej cievky, ktorej priemer je r , prierez S , má N závitov a je navinutá na jadre s permeabilitou m (obr.).
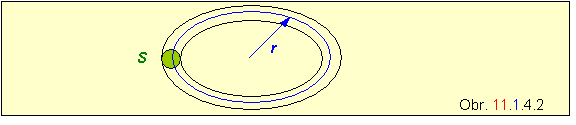
Riešenie Najprv treba vypočítať intenzitu magnetického poľa a magnetickú indukciu v cievke. Použijeme na to zákon celkového prúdu:
![]()
Magnetický tok cez jeden závit toroidu je F1 = BS , cez všetky závity spolu F = NBS = = (m N 2 S I)/(2pr) , odkiaľ na základe vzorca 11.1.4.1 pre vlastnú indukčnosť L dostaneme
![]() (11.1.4.4)
(11.1.4.4)
Poznámka: Na základe vzorca pre vlastnú indukčnosť toroidálnej cievky môžeme získať vzorec pre vlastnú indukčnosť veľmi dlhého solenoidu, keď namiesto obvodu 2pr dosadíme dĺžku solenoidu l .
Príklad 11.1.4.1 Vypočítajte koľko závitov by musela mať cievka s tvarom toroidu bez feromagnetického jadra, aby mala vlastnú indukčnosť L= 0,1 H ? Prierez toroidu S = 1 cm2 , stredný polomer r = 2 cm .
Riešenie Na výpočet použijeme vzorec (11.1.4.4), z ktorého pre počet závitov N dostaneme N = sqrt( L 2¶r / Smo ) , lebo v toroide mr = 1 . Po dosadení hodnôt dostaneme výsledok N = 104 závitov.
Kontrolné otázky
- Definujte veličinu vzájomná indukčnosť
- Definujte veličinu vlastná indukčnosť
- Ako sa vyjadruje indukované napätie na cievke s vlastnou indukčnosťou L ?
- Ako sa volá jednotka vlastnej indukčnosti v sústave SI ?
- Ktorá cievka má jednotkovú vlastnú indukčnosť ?
