 Magnetická energia vodiča ktorým preteká elektrický prúd
Magnetická energia vodiča ktorým preteká elektrický prúd
Uvážime jednoduchý elektrický obvod, pozostávajúci zo zdroja jednosmerného prúdu s elektromotorickým napätím Uem a cievky, ktorej vinutie má elektrický odpor R a vlastnú indukčnosť L .
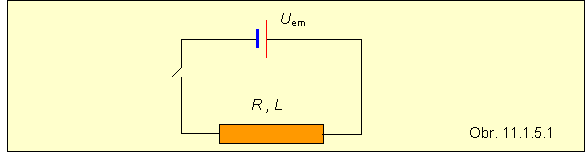
Po zopnutí kľúča začne obvodom tiecť elektrický prúd, pričom pomery v obvode opíšeme druhým Kirchhoffovým zákonom :
![]() ,
,
ktorý prispôsobíme nášmu prípadu. V obvode je zaradený jediný ohmický odpor R , takže na pravej strane rovnice zostane iba člen R I . V obvode však pôsobia dva zdroje elektromotorického napätia - jednosmerný zdroj s napätím Uem a cievka, v ktorej sa pri zmene prúdu indukuje napätie Ui = - L (dI / dt) . Po dosadení do Kirchhoffovho zákona dostaneme rovnicu :
Uem - L (dI / dt) = RI ,
ktorú vynásobíme elementom elektrického náboja dQ = I dt . Tak dostaneme rovnicu
Uem dQ - L (dI / dt) I dt = RI 2 dt ,
ktorú budeme integrovať :
![]()
Na ľavej strane rovnice je energia, ktorú zdroj jednosmerného napätia dodal do obvodu spolu s nábojom Q . Posledný člen rovnice (na pravej strane) predstavuje Jouleove straty, ktoré vznikli v časovom intervale (0, t ). Prostredný člen v rovnici po uskutočnení integrácie má tvar

a predstavuje energiu magnetického poľa, ktoré sa vytvorilo v cievke, resp. v okolí vodiča s indukčnosťou L , ktorým preteká prúd I .
Vo vnútri cievky je magnetické pole silnejšie, mimo cievky slabne so vzdialenosťou. Preto má význam zaviesť veličinu (objemová) hustota magnetickej energie , ktorá vyjadruje energiu pripadajúcu na objemovú jednotku. Túto veličinu zavedieme pomocou výpočtu magnetickej energie v toroide, kde magnetické pole sa nachádza iba vnútri toroidu, mimo neho je magnetické pole nulové.
Príklad 11.1.5.1 Vypočítajte magnetickú energiu toroidu, pozostávajúceho z N závitov navinutých na jadre kruhového prierezu s obsahom S , stredným polomerom toroidu r a vyrobeného z materiálu s permeabilitou m . (Obrázok, aj čiastkové výsledky - pozri príklad 11.1.4.1)
Riešenie Do vzorca pre magnetickú energiu dosadíme výsledky riešenia príkladu 11.1.4.1 :
Em = (1/2)[L]I 2 = (1/2) [mSN2 / 2pr ] I 2 = (1/2) (mNI / 2pr ) (N I / 2pr ) (S2pr ) ,
kde (mNI / 2pr ) = B je veľkosť vektora magnetickej indukcie v toroide, (N I / 2pr ) = H veľkosť vektora intenzity magnetického poľa v toroide a (S2pr ) predstavuje približne objem toroidu. Ak rovnicu vydelíme objemom toroidu, dostaneme magnetickú energiu pripadajúcu na jednotkový objem :
wm = Em / (S2pr ) = (1/2) BH (11.1.5.2)
Poznámka: Veľkosť vektorov B a H uvedená v príklade je presná iba pre kružnicu s polomerom r , ktorú sme situovali do stredu prierezu toroidového jadra. Smerom k okraju toroidu sa polomer kružníc zväčšuje, preto veľkosti vektorov sa zmenšujú. Presný postup by preto vyžadoval integráciu. Výsledok pre objemovú hustotu magnetickej energie je však správny a je rovnaký, ako by sme získali presným postupom integráciou. Pri presnom odvodení sa možno presvedčiť, že vo výraze pre hustotu magnetickej energie vystupuje skalárny súčin vektorov:

Kontrolné otázky
- Ako vzniká magnetická energia v okolí vodiča ?
- S ktorou mocninou elektrického prúdu sa mení magnetická energia v okolí vodiča ?
- Napíšte vzťah pre objemovú hustotu magnetickej energie !
- Slovne uveďte, čo rozumieme pod objemovou hustotou magnetickej energie !
- Aké napätie sa indukuje v cievke, keď sa mení veľkosť el. prúdu ktorý ňou preteká ?
