 Poyntingov vektor
Poyntingov vektor
Je to vektor, ktorý svojou veľkosťou predstavuje hustotu toku energie, ktorú prenáša elektromagnetická vlna. Inak povedané - ide o veličinu vyjadrujúcu koľko energie prenesie elektromagnetická vlna cez plochu s jednotkovým obsahom za jednotku času (plocha musí byť postavená kolmo na smer šírenia vlny). Poyntingov vektor P sa vyjadruje vzorcom

kde E je vektor intenzity elektrického poľa a H vektor intenzity magnetického poľa. Z fyzikálnych rozmerov vektorov E a H vyplýva, že rozmer Poyntingovho vektora je watt na štvorcový meter :
![]() (11.3.3.2)
(11.3.3.2)
Rozmerom veličiny sa potvrdzuje, že ide o prenos výkonu cez plochu s jednotkovým plošným obsahom.
Táto veličina - (plošná) hustota toku elektromagnetickej energie - sa niekedy nazýva aj intenzita elektromagnetického vlnenia .
Vzhľadom na význam tejto veličiny je potrebné podrobnejšie sa zaoberať odvodením vzorca (11.3.3.1).
Najprv vzorec odvodíme zjednodušeným spôsobom. Predstavíme si potrubie, ktorým prúdi energia. Na objemovú jednotku nech pripadá energia w (J/m3), ktorá prúdi potrubím rýchlosťou c , potrubie nech má prierez S . Za časový interval Dt energia postúpi potrubím o
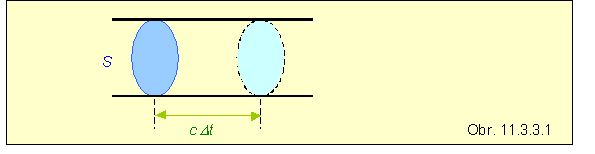
dĺžku cDt , takže zaplní objem S cDt . Vynásobením tohto objemu objemovou hustotou energie w dostaneme energiu, ktorá prešla prierezom S za časový interval Dt :
W = wScDt .
Keď túto energiu vydelíme plošným obsahom prierezu S a časovým intervalom Dt , dostaneme veličinu, vyjadrujúcu koľko energie prešlo jednotkovým plošným obsahom za jednotku času, t.j. hustotu toku energie P :
![]() (11.3.3.3)
(11.3.3.3)
Teraz môžeme dosadiť objemovú hustotu energie elektromagnetického poľa podľa vzorca (11.2.3.9) :
w = (1/2)ED + (1/2)BH (11.3.3.4)
pričom predpokladáme, že ide o izotropné prostredie, v ktorom je vektor E rovnobežný s vektorom D a vektor B s vektorom H , takže namiesto ich skalárneho súčinu možno napísať len súčin ich veľkostí. Vzorec pre hustotu energie ďalej upravíme pre prípad rovinnej elektromagnetickej vlny, v ktorej platí vzorec (11.3.2.6) , ktorý pre veľkosti vektorov B a E poskytuje vzťah : B = E / c . Tento vzťah ešte upravíme pre prípad vo vákuu, kde D = eoE a B = moH :
![]()
Výsledok využijeme pri úprave vzorca pre hustotu toku energie :
![]()
Získali sme vzorec pre veľkosť hustoty toku elektromagnetickej energie :

Vzorec nezohľadňuje vektorový charakter hustoty toku energie. Precízny spôsob jeho odvodenia - teda odvodenie Poyntingovho vektora - nájdete v nasledujúcom paragrafe.
Príklad 11.3.3.1 Odporová špirála je zhotovená z drôtu, ktorý má priemer d = 0,6 mm a dĺžku l = 2 m. Jej elektrický odpor je 5 W a prechádza ňou prúd I = 2 A . Vypočítajte veľkosť Poyntingovho vektora, vyjadrujúceho príkon elektromagnetickej energie do vodiča jeho povrchom.
Riešenie Joulove straty v špirále sú RI2 = 20 W . Tieto straty sú kompenzované prítokom elektromagnetickej energie povrchom špirály, ktorý má veľkosť S = 2prl = 3,77.10-2 m2 . Keď vydelíme Joulove straty veľkosťou povrchu špirály, dostaneme veľkosť Poyntingovho vektora : P = 20W / 3,77.10-2 m2 = 530,5 W/m2 .
Kontrolné otázky
- Čo vyjadruje Poyntingov vektor ?
- Napíšte vzorec Poyntingovho vektora !
- Ako súvisí Poyntingov vektor s hustotou elektromagnetickej energie ?
- Určte rozmer Poyntingovho vektora !
