 Žiarenie telies
Žiarenie telies
Tepelné žiarenie
Každý objekt pri danej teplote emituje žiarenie, ktoré nazývame tepelným žiarením. Charakter tohto žiarenia závisí od teploty a vlastností objektu. O existencii tepelného žiarenia sa každý z nás môže presvedčiť napríklad, ak do určitej vzdialenosti od pece, v ktorej sa začína kúriť, priložíme ruku. Čím dlhšie intenzívne kúrime, teplota pece vzrastá a rukou i bez dotyku túto zvyšujúcu teplotu pociťujeme. Obdobným dôkazom môže byť sledovanie teploty predmetu uloženého do blízkosti zohrievajúcej sa pece.
K popisu žiarenia si definujeme potrebné pojmy a fyzikálne veličiny:
q žiarivý tok f = dEc/dt jednotka W;
Žiarivý tok f - energia vyžiarená telesom za jednotku času (resp. výkon vyžiarený, absorbovaný, alebo prenášaný vlnením);
q intenzita vyžarovania (excitácia) M = d f/dS jednotka W.m-2;
M – energia vyžiarená jednotkovou plochou za jednotku času;
q spektrálna hustota (koncentrácia) intenzity vyžarovania Ml = d M/dl jednotka W.m-2;
Ml – energia vyžiarená jednotkovou plochou za jednotku času, ktorá pripadá na vlny z intervalu vlnových dĺžok <l,l+dl>.
q spektrálna hustota (koncentrácia) intenzity vyžarovania Mf = d M/df jednotka W.m-2;
Mf – energia vyžiarená jednotkovou plochou za jednotku času, ktorá pripadá na vlny z intervalu frekvencií <f,f+df>.
Pritom platí
![]() . (13.1.2.1)
. (13.1.2.1)
Experimentálne pozorované rozloženie spektrálnej hustoty intenzity tepelného vyžarovania Ml (obr. 13.1.2.1) ukazuje, že spektrum je spojité a rozprestiera sa v intervale vlnových dĺžok od infračervenej, viditeľnej až do ultrafialovej oblasti spektra. Všimnime si, že celkové emitované žiarenie (plocha pod krivkou) vzrastá so vzrastajúcou teplotou T.
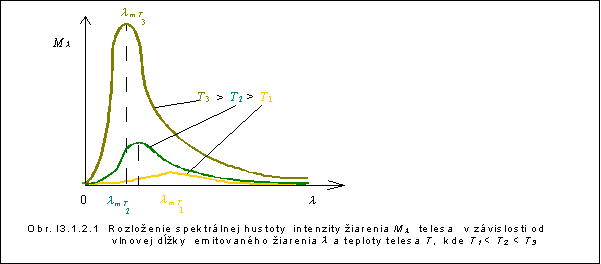
Pri nízkych teplotách vlnové dĺžky tepelného žiarenia spadajú hlavne do infračervenej oblasti, takže nie sú ľudským okom pozorovateľné. Pri určitej teplote teleso vyžaruje elektromagnetické vlnenie z oblasti viditeľnej časti spektra, ktoré možno registrovať ľudským okom. Pri nižších teplotách teleso sa rozpáli do červena. So zvyšujúcou sa teplotou sa jeho farba mení cez oranžovú, žltú až na bielu. Ak je svetlo červené, znamená to, že väčšina energie žiarenia pripadá na dĺžky vĺn, ktoré zodpovedajú červenému koncu spektra (760 nm). Ako farba postupne prechádza k bielej, maximum vyžarovanej energie sa presúva ku kratším vlnovým dĺžkam. Súvis teploty s farbou tepelného žiarenia (Tab. 13.1.2.1) sa využíva v niektorých prípadoch na určovanie približnej hodnoty teploty skúmaného objektu (napr. tavba vo vysokej peci ).
Tab. 13.1.2.1 Odhad teploty telesa na základe farby tepelného žiarenia
|
Farba |
Teplotný interval [ 0 C] |
|
náznak červenej |
500 – 550 |
|
tmavo červená |
650 – 750 |
|
jasno červená s nádychom oranžovej |
850 – 950 |
|
červená s nádychom do žlta |
1 050 – 1 150 |
vznikajúca biela |
1 250 – 1 350 |
|
biela |
1 450 – 1 550 |
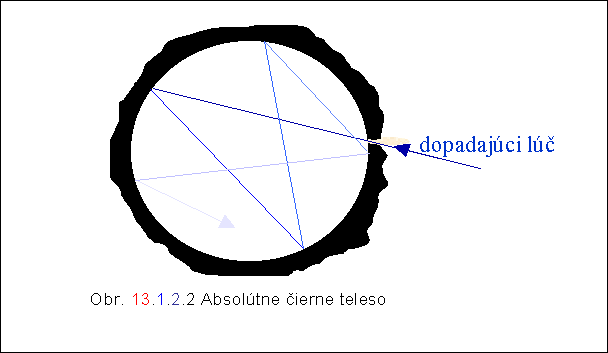
Aby sme sa pri skúmaní tepelného žiarenia nemuseli starať o konkrétnu povahu žiariaceho objektu, zavádza sa pojem absolútne čierne teleso. Absolútne čierne teleso je teleso, ktoré v tepelnej rovnováhe so svojím okolím absorbuje z okolia všetko dopadajúce žiarenie bez ohľadu na jeho vlnovú dĺžku (koeficient absorbcie a = 1) a rovnaké množstvo energie stenami do priestoru emituje. Výhodou absolútnych čiernych telies je, že sa chovajú naprosto rovnako. Absolútne čierne teleso si možno predstaviť ako duté teleso s dokonale odrážajúcimi stenami, napr. guľa o polomere R s malým otvorom (obr. 13.1.2.2). Žiarenie vstupujúce otvorom do dutiny po mnohonásobných odrazoch od jej stien odovzdá telesu celú svoju energiu. Ak steny majú teplotu T, žiarenie, ktoré zo zohriatych stien vychádza do priestoru nazývame žiarením absolútne čierneho telesa. Ak teleso absorbuje len časť dopadajúcej energie t.j. koeficient absorbcie a nadobúda hodnotu z intervalu (0, 1), hovoríme o žiarení sivého telesa.
Z rozloženia vyžiarenej spektrálnej hustoty intenzity tepelného vyžarovania Ml (obr. 13.1.2.1) vidieť, že so vzrastajúcou teplotou objektu maximum tepelného žiarenia sa posúva ku kratším vlnovým dĺžkam, čo vyjadruje tzv. Wienov posuvný zákon (13.1.2.2).
![]()
kde lmax je vlnová dĺžka, pri ktorej intenzita žiarenia Ml pri danej teplote T je maximálna. Z experimentálnych meraní spektrálnej hustoty intenzity vyžarovania Ml Stefan a Boltzmann zistili, že energia vyžiarená jednotkovou plochou za jednotku času je úmerná štvrtej mocnine absolútnej teploty stien dutiny. Tento poznatok poznáme ako Stefanov – Boltzmannov zákon:
![]() (13.1.2.3)
(13.1.2.3)
kde hodnota Stefanovej – Boltzmannovej konštanty s = 5,67 . 10-8 W m-2 K-4. Celková vyžiarená energia Ee plochou S za dobu t pri konštantnej teplote T je určená vzťahom
![]() . (13.1.2.4)
. (13.1.2.4)

Príklad 13.1.2.1 Maximum spektrálnej hustoty vyžarovania pripadá na vlnovú dĺžku 800 nm. Plocha povrchu telesa S = 100 cm2. Ako veľký musí byť príkon, aby toto teleso bolo udržované na stálej teplote T vo vnútri veľkej vyčerpanej nádoby, ktorej steny majú teplotu T1= 300 K? Straty tepla vedením zanedbajte.
Riešenie Aby teleso bolo udržiavané na stálej teplote T musíme mu dodať také množstvo energie, ktoré sa rovná rozdielu ním vyžiarenej energie a telesom prijatej energie vyžarovanej stenami nádoby o teplote T1. Energia vyžiarená za jednotku času určuje výkon P0 a energia prijatá za jednotku času určuje príkon P1. Rozdiel výkonu a príkonu môžeme určiť pomocou Stefanovho- Botzmannovho zákona (13.1.2.3) ako
![]() . (1)
. (1)
Z Wienovho posuvného zákona určeného vzťahom (2.1) vyjadríme T0
![]() . (2)
. (2)
Po dosadení číselných hodnôt dostávame
![]() .
.
Porovnaním teploty T0 s teplotou T1 zistíme, že T0 >> T1 a preto nemusíme energiu vyžiarenú stenami nádoby uvažovať. V dôsledku tejto aproximácie dostaneme pre príkon vzťah
![]() . (3)
. (3)
Po dosadení (2) do (3) dostávame
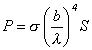 ,
,
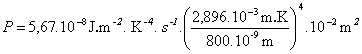 .
.
P = 97,498 kW
Príklad 13.1.2.2 Vypočítajte strednú teplotu Zeme, keď žiari ako absolútne čierne teleso, pričom vyžiarená energia je v rovnováhe s energiou, ktorú Zem prijíma od Slnka. Priemer Slnka vidíme zo Zeme pod uhlom a = 30¢, teplota povrchu Slnka je TS = 5 800 K. Zanedbajte teplo, pochádzajúce z vnútorných zdrojov Zeme.
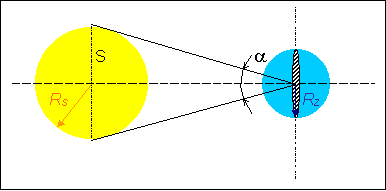
Riešenie Základným zákonom, z ktorého budeme vychádzať je zákon zachovania energie. Zem vyžiari toľko energie, koľko prijme od Slnka. Slnko zo svojho povrchu
![]()
vyžiari za jednu sekundu do celého okolitého priestoru energiu určenú Stefanovým- Botzmannovým zákonom
![]() ,
,
kde RS je polomer Slnka. Vo vzdialenosti d od Slnka dopadne na jednotkovú plochu energia
![]() .
.
Energia zo Slnka dopadá len na ožiarenú stranu Zeme (tú, kde je deň). Druhá (nočná) strana len vyžaruje, čo má za následok pokles teploty v noci, nakoľko Zem nie je až tak dobrý tepelný vodič. Nás zaujíma priemet povrchu osvetlenej plochy zemskej polgule do smeru kolmého na dopadajúce slnečné lúče, ktorým je kruh o ploche p RZ2 . Na povrch Zeme dopadne energia
![]()
kde d považujeme za vzdialenosť Zeme od Slnka a RZ je polomer Zeme, p RZ2 je priemet povrchu osvetlenej zemskej polgule do smeru kolmého na dopadajúce lúče. Zem vyžiari za sekundu energiu
![]() .
.
Zo zákona zachovania energie platí rovnosť medzi dopadnutou (prijatou) energiou zo Slnka na Zem a vyžiarenou energiou zo Zeme, t.j. E =EZ. Pre energiu vyžiarenú zo zeme opäť použijeme Stefanov-Botzmannov zákon. Po dosadení dostaneme
![]()
Pre strednú teplotu povrchu Zeme Tz dostaneme vzťah
![]()
![]()
![]()
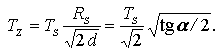
Po dosadení číselných údaj dostaneme výsledok pre Tz
![]() ,
,
resp. tZ = -2,25 0C.
Výsledok nám ukazuje, že v prípade ak zanedbáme vnútorné zdroje Zeme a Zem by prijímala energiu len zo Slnka, priemerná teplota Zeme, by bola pod bodom mrazu.
Príklad 13.1.2.3 Elektrický prúd prechádza tenkou chrómniklovou doštičkou šírky a = 0,01 m , hrúbky d = 10-5 m a dĺžky l. Relatívna pohltivosť povrchu doštičky (faktor absorbcie) je a = 0,34 . Pri akej veľkosti prúdu bude doštička najefektívnejším zdrojom viditeľného svetla, ak vieme, že ľudské oko je najcitlivejšie na žiarenie vlnovej dĺžky l = 550 nm a merný odpor materiálu doštičky je r =10-6 W.m?
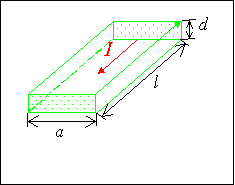
Riešenie Povrch doštičky vyžiari za jednu sekundu energiu E1 = a M , kde M je určená Stefanovým - Boltzmannovým zákonom (13.1.2.3). V stave rovnováhy príjme doštička za jednu sekundu energiu vo forme Jouleovho tepla
E2 = R I 2 ,
pričom platí
E1 = E2 Þ a M S = R I 2.
Vyjadríme povrch S a odpor R doštičky dĺžky l. vzťahom
![]() ,
,
kde prierez doštičky Sv = ad a S povrch doštičky, daný vzťahom
S = 2.( a + d) l.
Pre veľkosť prúdu I možno napísať
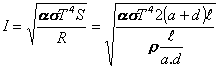 .
.
Z Wienovho posuvného zákona, vzťah (13.1.2.2), vyjadríme teplotu T = b/l. Pre hľadaný prúd získame vzťah
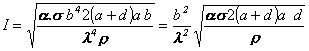 .
.
Po dosadení číselných údajov dostaneme pre veľkosť prúdu I = 171,77 A.
a) energiu vyžiarenú vláknom za jednotku času,
b) dobu, za ktorú po vypnutí prúdu poklesne teplota vlákna na izbovú teplotu (293 K ), pričom vlákno neprijíma z okolia žiadnu energiu a všetky nežiarivé tepelné straty možno zanedbať. Hustota vlákna je r =19.103 kg.m-3 a merná tepelná kapacita wolfrámu je c =54,88 J. kg-1.K-1.
Riešenie a) Celkové množstvo vyžiarenej energie za jednotku času jednotkovou plochou absolútne čierneho telesa zohriateho na teplotu T určuje Stefanov-Boltzmannov zákon daný vzťahom (13.1.2.3)
M0 = s T4 ,
kde s = 5,67. 10-8 J.s-1.m-2. K-4. Povrch vlákna s polomerom r a dĺžkou l vyžiari za jednotku času energiu
M = s T4 2p rl .
Na určenie neznámej teploty vlákna využijeme rovnicu (13.1.2.2) T = b/ l max. Pre energiu, ktorú vyžiari povrch vlákna za jednotku času získame, po využití uvedených rovností, vzťah
![]()
a po číselnom vyjadrení
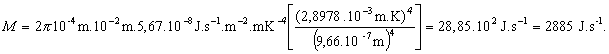
b) Ak vlákno stráca energiu len vyžarovaním, pokles teploty vlákna o dT nastane za časový interval dt, pričom zo zákona zachovania energie vyplýva
Mdt = -mcdT .
Po využití vzťahov a vyjadrení hmotnosti m = r V, pre energiu vyžiarenú z povrchu vlákna za dobu dt dostaneme
2p rl sT4dt= -m c dT .
Po separácii premenných
![]() ,
,
následnom integrovaní
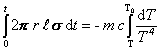 ,
,
a úprave dostaneme pre čas t
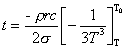 ,
,
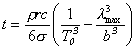 .
.
Po dosadení číselných hodnôt pre čas t dostaneme
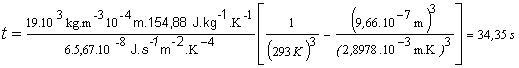
Kontrolné otázky
- Vysvetlite pojem tepelné žiarenie telesa.
- Do ktorej oblasti vlnových dĺžok spadá žiarenie telesa pri nízkych teplotách? Je toto žiarenie registrované ľudským okom?
- Ktoré veličiny sa používajú pri popise tepelného žiarenia?
- Ukážte, že jednotkou spektrálnej hustoty intenzity vyžarovania Mf je J.m-2.
- Nakreslite graf závislosti spektrálnej hustoty intenzity vyžarovania ako funkciu vlnovej dĺžky pri dvoch rôznych teplotách.
- Definujte pojem absolútne čierne teleso.
- Kedy hovoríme o sivom telese?
- Akú zaujímavosť zistil Wien pri skúmaní spektier zahriatych telies?
- Formulujte Wienov posuvný zákon.
- Vyslovte Stefanov-Boltzmannov zákon?
- Ako je definovaná veličina žiarivý tok?
- Ako sa nazýva veličina Ml?
- Nakreslite rozloženie Mf ako funkciu frekvencie žiarenia.
