Počet jadier dN, ktoré sa v priebehu času dt premenia závisí od počtu ešte nepremenených jadier N v čase t, od časového intervalu dt a od pravdepodobnosti premeny l: dN = -l N dt,

Po separovaní premenných a integrovaní:

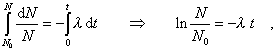
dostaneme zákon premeny, udávajúci závislosť počtu ešte nepremenených rádionuklidov po uplynutí času t v tvare:

(14.2.2.1)

kde N₀ je počiatočný počet nuklidov nestabilného izotopu v čase t = 0 s. Tento zákon premeny má štatistický charakter a preto platí presne len pre veľký počet jadier N₀. Ak vezmeme do úvahy definíciu doby polpremeny T_1/2, bude mať zákon (14.2.2.1) v čase t = T_1/2 tvar:

odkiaľ dostávame súvis medzi dobou polpremeny a konštantou premeny:

(14.2.2.2)

Zákon premeny môžeme potom písať v tvare:

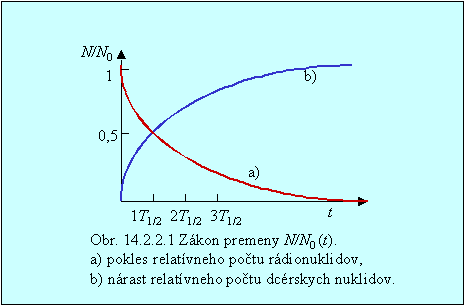
Na obr. 14.2.2.1 je znázornený pokles relatívneho počtu rádionuklidu (krivka a) a súčasne nárast relatívneho počtu dcérskeho nuklidu (krivka b), vznikajúceho premenou pôvodného rádionuklidu.

Pre aktivitu, teda rýchlosť premeny v ľubovoľnom čase t dostaneme:

(14.2.2.3)

kde A₀ je rýchlosť premeny v čase t = 0 s.

Príklad 14.2.2.1 Rádioaktívny jód ¹²⁸I sa používa v medicíne pri vyšetreniach štítnej žľazy. Pri meraniach rýchlosti premeny tohto rádionuklidu sme namerali aktivitu A₁ = 390 Bq po 4 minútach od jeho aplikácie a aktivitu A₂ = 27 Bq po 100 minútach. Aká je počiatočná aktivita, konštanta premeny, doba polpremeny a stredná doba života tohto rádionuklidu?

Riešenie: Pre aktivitu platí vzťah (14.2.2.3), v našom prípade pre aktivitu A₁ v čase t₁ a aktivitu A₂ v čase t₂ môžeme písať:

Predelením týchto rovníc dostaneme:

Po logaritmovaní rovnice a úprave dostaneme konštantu premeny:

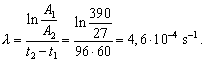
Stredná doba života tohto rádionuklidu je:

Doba polpremeny:

Počiatočnú aktivitu môžeme vyjadriť z pôvodnej rovnice:

Príklad 14.2.2.2 Za aký čas klesne aktivita rádioaktívneho ²⁴Na na jednu desatinu počiatočnej hodnoty, ak doba polpremeny sodíka je T_1/2 = 15,0 h?

Riešenie: Aktivita v čase t je A a keďže A = 0,1 A_{0 ,} dostaneme:

Odtiaľ vyjadríme čas:

Príklad 14.2.2.3 Vypočítajte počet nuklidov, ktoré sa premenia za sekundu, ak žiaričom je 1 gram čistého rádioaktívneho kobaltu ⁶⁰Co, ktorého doba polpremeny je T_1/2 = 5,3 rokov?

Riešenie: Počet nuklidov, ktoré sa premenia za sekundu udáva aktivita žiariča. Súvis medzi aktivitou a celkovým počtom nuklidov vyjadruje vzťah (14.2.2.3)

v tvare:

kde konštanta premeny súvisí s dobou polpremeny:

a počet nuklidov N je rovný počtu atómov v množstve látky hmotnosti m = 0,001 kg, ktorej molárna hmotnosť je M:

kde N_A je Avogadrova konštanta. Potom:

Teda počet nuklidov, ktoré sa premenia za sekundu je 4,2×10¹³.

Pre jadrové premeny platia zákony zachovania elektrického náboja a počtu nukleónov, z ktorých vychádzajú Soddyho-Fajansove pravidlá posunu izotopov. Pre jednotlivé druhy premien majú nasledovný tvar:

a - premena

Pri tejto samovoľnej premene jadra sa emituje a- častica, tj. jadro hélia, dcérsky nuklid má atómové číslo o 2 jednotky a hmotnostné číslo o 4 jednotky menšie ako materský nuklid:

(14.2.2.4)

b - premena

b - premena je najrozšírenejší proces jadrovej premeny. Pojem b - premena zahŕňa tri možné druhy premeny, pričom pri každej z nich sa mení elektrický náboj jadra a teda atómové číslo Z o jednotku. Ide o elektrónovú b^- - premenu, pozitrónovú b⁺ - premenu a K – záchyt elektrónu.

Symbolický zápis b^- - premeny má tvar:

(14.2.2.5)

Pri b^- - premene sa z jadra emitujú elektróny (ktoré nie sú súčasťou jadra!), vznikajúce vnútri jadra tým, že sa premieňa neutrón podľa rovnice:

(14.2.2.6)

b⁺ - premenu môžeme vyjadriť:

(14.2.2.7)

Pri pozitrónovej b⁺ - premene nastáva emitovanie pozitrónu (pozitrón je antičastica k elektrónu, má rovnakú hmotnosť ale kladný náboj), ktorý vzniká v jadre v dôsledku premeny protónu podľa vzťahu:

(14.2.2.8)

Symboly ΰ, n v rovniciach (.2.11) a (.2.13) sú elektrónové antineutríno a neutríno – subnukleárne častice s takmer nulovou hmotnosťou, odnášajúce časť energie, uvoľnenej pri premene jadra.

Záchyt orbitálneho elektrónu

nastáva, keď jadro obsahuje o jeden protón viac ako pripúšťa jeho stabilita, zachytí jeden orbitálny elektrón. Najčastejšie ide o K-záchyt, pretože pravdepodobnosť záchytu elektrónu je úmerná pravdepodobnosti, s ktorou sa nachádza elektrón v blízkosti jadra. Protón v jadre sa premení na neutrón a uvoľní sa neutríno, uvoľnené miesto elektrónu sa zaplní elektrónom z vyššej hladiny a prebytok energie sa vyžiari vo forme fotónu. Schéma orbitálneho záchytu:

(14.2.2.9)

(14.2.2.10)

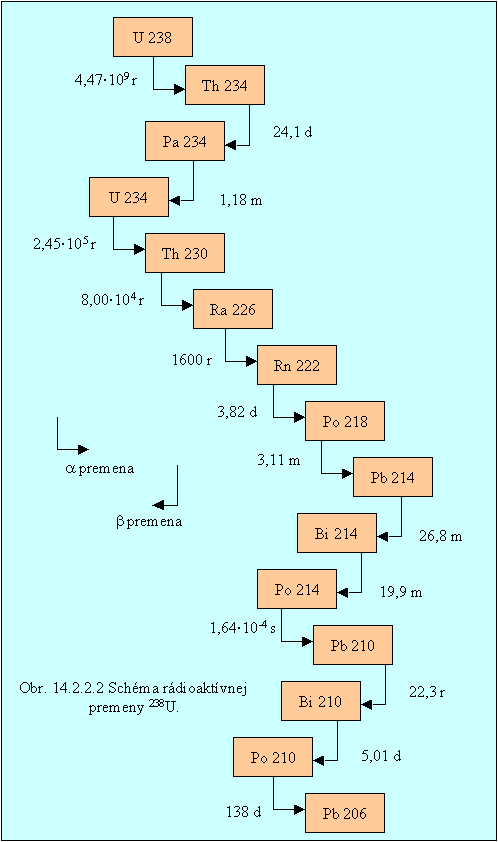
Na základe týchto pravidiel môžeme zoskupiť rádioaktívne izotopy do istých geneticky viazaných skupín, tzv. rádioaktívnych premenových radov. Ide o rad prvkov, ktorý vzniká postupne premenou základného prvku. Každý rad začína dlhožijúcim izotopom najťažšieho prvku radu a končí stabilným izotopom najľahšieho z nich (ide o izotopy olova, resp. bizmutu). Sú možné 4 rady: urán-rádiový ²³⁸U, thóriový ²³²Th, aktíniový ²³⁵U a neptúniový ²³⁷Np. Na obr. 14.2.2.2 je schéma uránového premenového radu.

Príklad 14.2.2.4 Koľko častíc alfa a beta sa emituje pri úplnej premene 2×10^–5 mg ²³⁸U na stabilné ²⁰⁶Pb?

Riešenie  Na základe zákonov zachovania náboja a počtu nukleónov platí sumárna schéma premeny:

Vypočítame počet atómov v danej vzorke:

Počet emitovaných častíc a je n_a = 8N = 4,04×10¹¹ a počet emitovaných častíc b je n_b = 6N = 3,03×10¹¹.