Coulombov zákon
Coulombov zákon
Vzájomné silové pôsobenie elektricky nabitých telies možno popísať pomerne jednoduchými vzťahmi, pokiaľ sa tieto telesá nachádzajú v pokoji - nepohybujú sa. Hovoríme, že telesá a častice sú statické, a preto celú túto oblasť javov nazývame elektrostatikou. Akonáhle sa nabité častice začnú pohybovať objavujú sa nové efekty - magnetické polia a pri ich zrýchlenom pohybe sa pozoruje dokonca vyžarovanie elektromagnetických vĺn. Tieto javy budú obsahom až ďalších kapitol tohoto kurzu.
Silové pôsobenie nábojov
V mechanike sme sa naučili, že najpresnejší spôsob merania síl predstavujú rovnoramenné váhy. S ich aplikáciou na meranie elektrických síl však rýchlo skončíme. Problém je v tom, že elektrické sily výrazne závisia od vzdialenosti, zatiaľ čo tiažové sily pôsobiace na závažia sú v rámci niekoľkých desiatok kilometrov od miesta váženia konštantné. Videli sme to už v prvom pokuse, keď sme sa s nabitým telesom približovali k drobným telieskam, že výrazný silový účinok sa začal prejavovať až pri priblížení sa na malú vzdialenosť 1 - 2 cm, ale potom sa prudko zvyšoval so zmenšujúcou vzdialenosťou.
Druhá možnosť na meranie síl je silomer, čiže zariadenie, ktoré využíva na meranie deformáciu struny. Nepresnosť silomerov je však veľká - cca 10 až 20 % a rozsah merania síl je malý, lebo pri väčších deformáciách struny sa začínajú prejavovať odchýlky od Hookovho zákona, únava materiálu a pod. Je tu ešte iná možnosť - využiť na meranie sily krútenie (torziu) dlhého tenkého vlákna. Prvé takéto zariadenie skonštruoval francúzsky fyzik Coulomb a po ňom dostalo toto zariadenie aj svoj názov - "Coulombove torzné váhy"
|
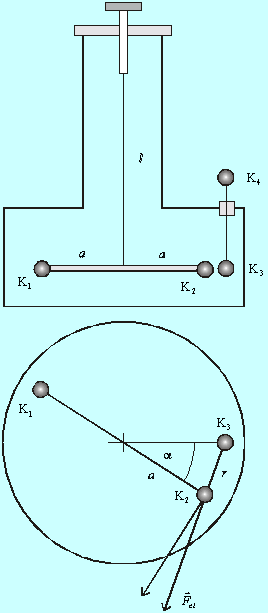
Obr. 1 Princíp Coulombových torzných váh |
Princíp torzných váh je znázornený na obr. 1.
Na tenkom pružnom vlákne dĺžky l a polomeru R je závesné izolačné ramienko dĺžky 2a. Na koncoch ramienka sú kovové guľôčky K1, K2 s rovnakým polomerom. Konštrukcia Coulombových torzných váh musí byť celkom symetrická, aby sa pôsobenie tiažových síl na guľôčky úplne vykompenzovalo.
V blízkosti guľôčky K2 je ďalšia kovová guľôčka K3 upevnená na tenkej kovovej tyčke. Táto guľôčka slúži na privedenie náboja z vonkajšieho priestoru prostredníctvom kovovej guľôčky K4. V počiatočnej polohe (ktorá sa dá nastaviť mechanizmom pri hornom úchyte vlákna) sú guľôčky K2 a K3 v dotyku. Nabitým telesom sa dotkneme guľôčky K4. Privedený náboj sa rozloží na povrchu guličiek K2, K3, K4. Ak sú ich polomery rovnaké, na každej z nich bude rovnaký elektrický náboj. (pozri nasledujúci kapitolu o kapacite vodičov). Celé váhy sú uzavreté v sklenenom obale, aby sa vylúčili rušivé vplyvy od prúdenia vzduchu.
Pôsobením elektrickej odpudivej sily sa guľôčka K2 vzdiali od guľôčky K3. Výsledné otočenie vahadla o uhol a odpovedá rovnováhe elektrickej a torznej sily deformovaného vlákna. Rovnovážna poloha ramienka je určená rovnováhou momentu Del odpudivej sily a torzného momentu vlákna Dtor .
![]() ,
, ![]()
Z toho
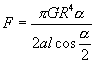
Náboj na pevnej guľôčke môžeme opakovane zvyšovať a tak porovnávať účinky nábojov rôznej veľkosti. Pri svojich pokusoch Coulomb dospel k týmto záverom:
1. Sily medzi nábojmi pôsobia v smere ich spojnice. Takéto sily nazývame centrálne.
2. Ak je jeden náboj konštantný, tak pôsobiaca sila je priamo úmerná veľkosti druhého náboja pri rovnakých vzdialenostiach r medzi nábojmi. Zo symetrie experimentu vyplýva, že celková sila je teda úmerná súčinu veľkosti oboch nábojov.
3. Pri rovnakej veľkosti nábojov je sila pôsobiaca medzi nimi nepriamo úmerná druhej mocnine ich vzdialenosti.
Coulombov zákon
Matematicky môžeme Coulombov zákon formulovať nasledovne:
![]() (8.1.3.2.1)
(8.1.3.2.1)
kde F21 je sila pôsobiaca na náboj q2 pochádzajúca od náboja q1 a r2 , r1 sú polohové vektory týchto nábojov. Pritom budeme vždy dodržiavať konvenciu, že prvý index určuje objekt, na ktorý sila pôsobí a druhý index je spojený s pôvodom tejto sily. Správne by sme mali indexy oddeľovať čiarkou, teda písať F2,1 avšak obyčajne, pokiaľ nie sú indexy vyššie ako číslica 9 a ich interpretácia je jednoznačná, tak sa používa zjednodušené označovanie bez oddeľujúcej čiarky.
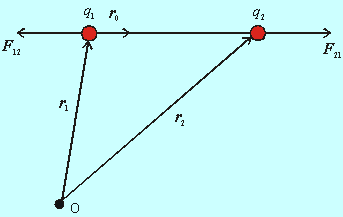
Obr. 8.1.3.2.1
Silové pôsobenie medzi dvoma nábojmi
Rovnica (8.1.3.2.1) rešpektuje vektorový charakter pôsobiacej sily a súčasne aj príťažlivý a odpudivý charakter sily v závislosti od výsledného znamienka súčinu nábojov. V menovateli formálne vystupuje tretia mocnina vzájomnej vzdialenosti nábojov, ale treba si uvedomiť, že výraz
![]()
vyjadruje jednotkový vektor v smere pôsobiacej sily.
Konštanta úmernosti k vo vzťahu (8.1.3.2.1) závisí od použitej sústavy jednotiek. V SI sústave platí:
![]() (8.1.3.2.2)
(8.1.3.2.2)
kde eo = 8,854.10-12 A2.kg-1 .m-3.s4. Veličinu e0 nazývame permitivitou vákua (niekedy sa nazýva tiež elektrická konštanta). Faktor 4p v menovateli je zavedený preto, aby nevystupoval v iných vzťahoch, ktoré vyplývajú z Coulombovho zákona. Tieto potom vyzerajú jednoduchšie a elegantnejšie.
Treba pripomenúť, že sily, ktoré vystupujú v Coulombovom zákone sú sily akcie a reakcie. Teda platí
F21 = - F12 (8.1.3.2.3)
Slovami môžeme Coulombov zákon formulovať nasledovne: Dva bodové náboje, ktoré sú v pokoji, pôsobia na seba silou, ktorá je priamo úmerná súčinu veľkostí nábojov a nepriamo úmerná druhej mocnine ich vzájomnej vzdialenosti.
Príklad 8.1.3.1 Dve uhlíkové guľôčky , z ktorých každá má hmotnosť 1 g a je nabitá záporným nábojom , sú zavesené v jednom bode na nitiach dlhých 10 cm. Silové pôsobenie má za následok, že sa nite rozostúpia o 60o uhol.
a) Akou elektrostatickou silou na seba guľôčky pôsobia?
b) Koľko elektrónov bolo prinesených na každú guľôčku pri nabíjaní?
c) Akou gravitačnou silou na seba guľôčky pôsobia?
Riešenie|
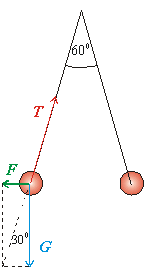
Obr.8.1.3.1 |
a) Súčet elektrostatickej odpudivej sily F, sily T ktorou niť pôsobí na guľôčku a tiaže guľôčky G sa musí rovnať 0.
tg 300 = F/ m.g
F = m.g. tg 300 =5,66.10-3 N
b) Z Coulombovho zákona dostaneme pre veľkosť náboja
q = 2r.(p.eo .F)1/2
z obrázku plynie
r = 2.l.sin 300 =0.1 m
potom q = 7.93.10-8 C
Počet elektrónov privedených na guľôčku je q/e = 7,93.10-8 C / 1,6.10-19 C = 4,896 .1011
c)Pre gravitačnú silu, ktorou na seba pôsobia 2 guľôčky s hmotnosťami 1g dostaneme
F = 6,67.10-11 . 10-6 /10-2 N = 6,67 .10-15 N
Vidíme, že elektrostatická odpudivá sila medzi guľôčkami je 8,5.1011 krát väčšia ako gravitačná príťažlivá sila , preto gravitačnú príťažlivú silu môžeme zanedbať.
Príklad 8.1.3.2 Vypočítajte klasickú obežnú rýchlosť elektrónu ,obiehajúceho okolo jadra atómu vodíka. Hmotnosť elektrónu je 9,1.10-31 kg. Polomer kruhovej dráhy elektrónu v atóme vodíka je podľa Bohra 0,52 .10-10 m.
Dostredivá sila sa rovná Coulombovej sile
![]()
Elektrostatickú silu počítame z Coulombovho zákona
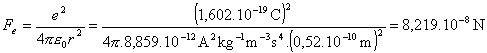 ,
,
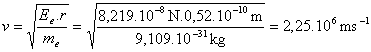
Rýchlosť elektrónu na obežnej dráhe je 2,25.106 m.s-1
Princíp superpozície
Skúmajme teraz, aké bude silové pôsobenie na náboj q v bode r od väčšieho počtu bodových nábojov q1, q2, … , qn, ktoré sa nachádzajú v bodoch r1, r2, …, rn. Sila pôsobiaca na tento náboj pochádzajúca od náboja qi je
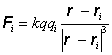 (8.1.3.3.1)
(8.1.3.3.1)
Experimenty ukazujú, že výslednú silu dostaneme ako vektorový súčet takýchto síl od všetkých pôsobiacich nábojov. Teda
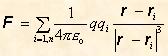 (8.1.3.3.2)
(8.1.3.3.2)
Vzťah (8.1.3.3.2) vyjadruje "princíp superpozície elektrických síl".
Príklad 8.1.3.3. Tri náboje -q sú umiestnené vo vrcholoch rovnostranného trojuholníka s dĺžkami strán a. Náboj Q je v jeho ťažisku.
a) Odvoďte výraz pre silu, ktorá pôsobí na jeden z nábojov -q. Určite smer tejto sily.
b) Aký musí byť vzťah medzi hodnotami nábojov ,aby sila pôsobiaca na náboj -q bola nulová? Je tento systém elektrických nábojov stabilný?
|
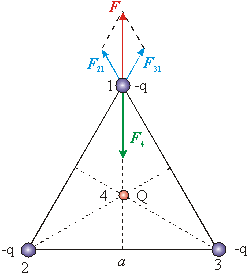
Obr 8.1.3.2 |
a) Na náboj –q v mieste 1 pôsobia náboje z miesta 2, 3 silami F21, F31 a náboj Q silou F4.
Výsledná sila Fv , ktorou tieto náboje pôsobia na náboj v mieste 1, je daná vektorovým súčtom .Možno písať
Fv = F4.+ F21 + F31
Podľa Coulombovho zákona veľkosť sily F21, F31 je
![]()
Veľkosť sily F podľa obrázka je
![]() .
.
Veľkosť sily F4 je
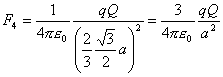
Pre veľkosť výslednej sily môžeme písať Fv =F- F4 .
b) Náboj Q umiestnený v ťažisku trojuholníka má opačný náboj, teda kladný .
Výsledná sila Fv je nulová, preto F = F4.
Dosadením dostaneme
![]()
z toho vzťah medzi nábojmi q, Q je
![]() .
.
Tento systém nábojov je labilný. Stačí, aby sa jeden z nábojov máličko vychýlil zo svojej polohy, a nastane pohyb nábojov, čím sa celý systém rozpadne. Vo všeobecnosti sa ukazuje, že nie je možné vytvoriť stabilnú rovnovážnu konfiguráciu nábojov, ktoré sú v pokoji.
Dostredivá sila sa rovná Coulombovej sile
![]() .
.
Elektrostatickú silu počítame z Coulombovho zákona
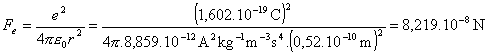 ,
,
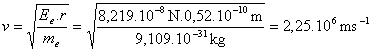
Rýchlosť elektrónu na obežnej dráhe je 2,25.106 m.s-1.
Rozsah platnosti Coulombovho zákona
V laboratórnych podmienkach môžeme Coulombov zákon priamym meraním overiť s presnosťou 0,1 %. Oveľa presnejšie sú nepriame metódy na základe vzťahov, ktoré vyplývajú z Coulombovho zákona, kde sa dosiahlo overenie s presnosťou asi na 7 platných cifier.
Na rozdiel od gravitačných síl, nemáme možnosti priamo overovať Coulombov zákon a pôsobenie elektrických síl v kozmických rozmeroch. Tu jeho platnosť iba extrapolujeme na základe konzistentnosti a funkčnosti celej elektrodynamiky, ktorá je vybudovaná na základe Coulombovho zákona.
V mikrosvete je Coulombov zákon určujúcim faktorom, pre správanie sa elektrónov v atómoch a molekulách. Tu sa dosahuje zhoda teoretických predpovedí a nameraných hodnôt na 10 platných cifier pri najpresnejších meraniach.
Otázku môžeme však položiť aj inakšie. Do akej miery je exponent v menovateli presne rovný číslu 2, či tu nie sú nejaké odchýlky napr. 1,9999, čo by sa prejavilo iba buď vo veľkých vzdialenostiach alebo na veľmi malých vzdialenostiach. Teória ukazuje, že v Coulombovom zákone je tento exponent presne 2,0000… V opačnom prípade by rýchlosť šírenia elektromagnetických vĺn vo vákuu závisela od frekvencie. Astronomické pozorovania žiarenia pulzarov a výbuchov supernov potvrdzujú konštantnosť rýchlosti svetla pre rôzne vlnové dĺžky, čím sa odchýlka exponentu od čísla 2 vylučuje.
Porovnanie elektrických a gravitačných síl
Aby sme mali bližšiu predstavu o úlohe, ktorú hrajú elektrické sily v prírode, porovnajme si veľkosť elektrickej a gravitačnej sily príťažlivej sily, ktorou na seba pôsobia protón a elektrón v atóme vodíka pre typickú vzdialenosť r = a0, čo je tzv. Bohrovský polomer rovný 0,52. 10-10 m.
![]()
= 6,67 . 10-11 Nm2kg-2 1,6726 . 10-27 kg . 9,11 . 10-31 kg / (0,52 . 10-10 m)2 = 3,7586 . 10-47 N (8.1.3.5.1)
![]()
= ( 1,602 . 10-19 C )2 / 4 . 3,14 . 8,854 .10-12 C2 N-1 m-2 . (0,52 . 10-10 m)2 = 8,5347 . 10-8 N (8.1.3.5.2)
Potom pre pomer Fe / Fg dostaneme
Fe / Fg = 2,27 . 1039 (8.1.3.5.3)
Teda elektrická sila je skoro o 40 rádov silnejšia ako gravitačná sila. Preto v mikrosvete, v štruktúre atómov a molekúl je rozhodujúca elektrická sila a nie gravitačná. Gravitačné efekty sú na tejto úrovni úplne zanedbateľné.