 Potenciál elektrostatického poľa
Potenciál elektrostatického poľa
Premiestňovanie náboja v elektrostatickom poli – práca
V tomto odseku sa budeme zaoberať premiestňovaním elektrických nábojov v elektrostatickom poli. Na začiatku sme vyhlásili, že celá kapitola sa týka iba elektrostatiky. To znamená, že sa zaoberáme iba takými javmi a procesmi, kde sú elektrické náboje a iné telesá v pokoji ( t.j. nemenia svoju polohu). Pritom sme taktne obišli kľúčový problém, odkiaľ sa berú nejaké "iné sily", ktoré držia celú sústavu nábojov pohromade, Tak napríklad sústredenie kladných nábojov v homogénne nabitej guli by sa pôsobením odpudivých elektrických síl rozpadlo v zlomku sekundy a náboje by sa rozleteli na všetky strany. Dá sa celkom všeobecne dokázať, že principiálne nie je možné vytvoriť stabilnú statickú konfiguráciu elektrických nábojov. Existenciu takejto inej sily musíme predpokladať aj pri manipulácii s testovacím nábojom v elektrickom poli. Jedine tak dosiahneme, že môžeme "v pokoji" merať elektrickú silu, ktorá naň pôsobí. Ďalšou etapou v našom bádaní je sledovať proces pomalého premiestňovania testovacieho náboja v elektrickom poli, tak aby nevznikali efekty súvisiace s pohybom náboja.
V celej ďalšej časti tejto kapitoly budeme teda predpokladať:
· Na testovací náboj q pôsobí v každom bode elektrická sila F(r) = qE(r)
· Okrem toho na teleso (časticu), ktoré nesie náboj q pôsobí iná sila F´, ktorá takmer úplne kompenzuje účinok elektrického poľa E. Ak je kompenzácia úplná, F´ = -F, náboj je v pokoji. Ak kompenzácia nie je úplná F´ ¹ -F, tak výsledná sila F´ + F ¹ 0 spôsobí malé zrýchlenie náboja a jeho pohyb. Aby sme sa čo najlepšie priblížili elektrostatike musí platiť F´ » -F. Vo všetkých ďalších úvahách budeme preto predpokladať, že táto iná sila F´ sa rovná -F s nejakou nesmierne malou (infinitesimálnou) odchýlkou, aby sme dosiahli čo najpomalšie presúvanie testovacieho náboja q z jedného miesta na druhé.
Obr. 8.1.10.1.1
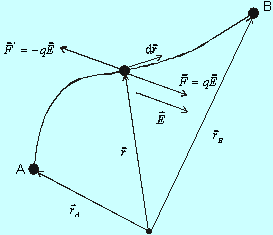
Premiestňovanie náboja v elektrickom poli.
Uvažujme teraz presun náboja q z miesta A určeného polohovým vektorom rA do bodu B (rB). Presun môžeme vykonať rôznym spôsobom, preto si naplánujeme nejakú trasu znázornenú krivkou C na obr.8.1.10.1.1
Celú trasu môžeme rozdeliť na nekonečne malé úseky dr. Na každom úseku pôsobíme na náboj silou F´ = -qE. Ak pôsobíme silou, tak pri posunutí náboja vykonáme prácu
![]() (8.1.10.1.1)
(8.1.10.1.1)
Celkovú prácu, ktorú pri premiestňovaní náboja q vykonáme dostaneme ako
![]() (8.1.10.1.2)
(8.1.10.1.2)
Vyskúšajme si tento postup na prípade, že zdrojom elektrostatického poľa je bodový náboja q1 umiestnený v začiatku súradnicovej sústavy. Vtedy
![]() (8.1.10.1.2.3)
(8.1.10.1.2.3)
Po dosadení do rovnice (8.1.10.1.2) dostaneme
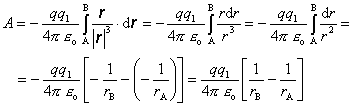 (8.1.10.1.2.4)
(8.1.10.1.2.4)
Pri odvodení sme využili skutočnosť, že
![]() (8.1.10.1.2.4)
(8.1.10.1.2.4)
lebo priemet vektora dr do smeru vektora r reprezentuje prírastok dr dĺžky tohoto vektora.
Elektrostatický potenciál
Výsledok (8.1.10.1.2.4), ku ktorému sme dospeli, je veľmi zaujímavý. Ukazuje, že práca, ktorú vykonáme pri premiestnení náboja q v poli E nezávisí od spôsobu premiestňovania - tvaru dráhy, ktorú pritom náboj vykoná, ale iba od začiatočnej a koncovej polohy. S niečím podobným sme sa už stretli v gravitačnom poli a výsledok ukazuje, že môžeme pre náboj q zaviesť funkciu U(r) - potenciálnu energiu náboja, pre ktorú platí
![]() (8.1.10.2.1)
(8.1.10.2.1)
Samozrejme hodnota tejto funkcie závisí od veľkosti náboja q. Preto je užitočné vydeliť túto funkciu veľkosťou náboja q, čím dostaneme veličinu, ktorá udáva potenciálnu energiu v prepočte na jednotkový náboj. Takúto veličinu budeme označovať písmenom j a nazývať elektrostatickým potenciálom náboja q1.
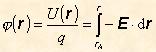 (8.1.10.2.2)
(8.1.10.2.2)
Tento potenciál vzťahujeme na nejaký referenčný bod rA . Špeciálne pre bodový náboj q1 umiestnený v začiatku súradnicovej sústavy dostaneme
![]() (8.1.10.2.3)
(8.1.10.2.3)
Pre elektrostatický potenciál bola zavedená samostatná jednotka volt, značka V. Rozmer tejto jednotky je J/C. Slovami môžeme povedať: medzi dvoma bodmi je rozdiel potenciálu 1 volt, ak pri prenose náboja 1 coulomb medzi týmito dvoma bodmi vykonáme prácu 1 joule.
Voľba referenčného potenciálu
Potenciálna energia U a potenciál j sú definované integrálnymi vzťahmi, a preto nie sú určené jednoznačne. Môžeme k nim pridať ľubovoľnú konštantu. Preto pri výpočtoch elektrostatického potenciálu musíme udať referenčný bod, vzhľadom na ktorý výpočet robíme. Obvykle uvažujeme nasledovne. Elektrické sily klesajú so vzdialenosťou. Ak sa testovací náboj nachádza v nekonečne, tak silové pôsobenie akéhokoľvek náboja naň je nulové. Preto je rozumné náboju v nekonečne veľkej vzdialenosti priradiť hodnotu potenciálu rovnú nule. Tým napríklad pre potenciál elektrického poľa od bodového náboja umiestneného v začiatku dostaneme
![]() (8.1.10.3.1)
(8.1.10.3.1)
Poznámky:
· Nie vždy je takáto voľba referenčného potenciálu možná. Napríklad pri problémoch s valcovou symetriou tento postup zlyháva a potenciál musíme vzťahovať na nejaký konkrétny bod, kde udáme jeho referenčnú hodnotu.
· Pri štandardnej voľbe nulovej hodnoty potenciálu v nekonečne, nadobúda rovnica (8.1.10.2.2) tvar
![]() (8.1.10.3.2)
(8.1.10.3.2)
· kde sme využili zmenu znamienka určitého integrálu pri zámene jeho medzí. Zo vzťahu (8.1.10.3.2) vyplýva, že potenciál môžeme tiež chápať ako prácu, ktorú vykonajú sily elektrického poľa pri premiestnení jednotkového náboja z daného bodu do nekonečna. Formálne sú obidva prístupy ekvivalentné a v učebniciach sa takto využívajú. Treba však pripomenúť, že pokiaľ by sme nechali na nejaký náboj q pôsobiť iba sily od elektrického poľa E, náboj sa bude pohybovať zrýchlene, začne vyžarovať a časť energie, ktorú získal, vyžiari do okolitého priestoru. Urobiť presnú energetickú bilanciu v takomto prípade je nad naše sily. Preto dávame v tomto texte prednosť takej definícii práce pri premiestňovaní náboja, kde je jasné, že tento proces prebieha pomaly a iné efekty sú vylúčené.
Často sa zaujímame o plochy, pre ktoré platí j ( r ) = konšt. Takéto plochy predstavujú plochy konštantného potenciálu alebo ekvipotenciálne hladiny. Využívajú sa na charakterizáciu elektrických polí v priestore.
Potenciál sústavy nábojov a spojitého rozloženia nábojov
Vzťah (8.1.10.3.1), ktorý sme dostali pre potenciál bodového náboja môžeme na základe princípu susperpozície elektrických polí ihneď zovšeobecniť na ľubovoľnú sústavu bodových nábojov qi :
![]() (8.1.10.4.1)
(8.1.10.4.1)
Pre spojité rozloženia nábojov s hustotou r(r´) máme
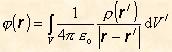
![]() (8.1.10.4.2)
(8.1.10.4.2)
a integrácia prebieha cez celý objem V, kde sa nachádzajú náboje. Pre náboje rozložené na ploche s plošnou hustotou s platí
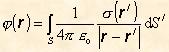 (8.1.10.4.3)
(8.1.10.4.3)
A pre náboje rozložené na vlákne s dĺžkovou hustotou l pozdĺž nejakej krivky C je
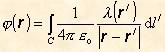 (8.1.10.5.4)
(8.1.10.5.4)
Vidíme, že vzťahy na výpočet potenciálu sú podstatne jednoduchšie ako vzťahy na výpočet elektrostatického poľa, čo sa v praxi veľmi často aj využíva. Potrebujeme nájsť len obrátený "recept" na výpočet elektrického poľa ak poznáme potenciál, čo bude predmetom nasledujúceho odseku.
Príklad 8.1.10.1 Dva bodové náboje Q1 = 8 mC, Q2 = 5 mC sú vo vzdialenosti d = 20 cm. V ktorom mieste na ich spojnici sú potenciály budené oboma nábojmi rovnaké?
Riešenie
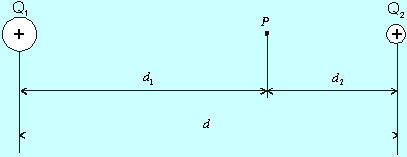
Obr.8.1.11.1
Potenciál bodového náboja Q1v bode P sa rovná
![]() ,
,
Potenciály sú rovnaké, čo znamená
![]() ,
,
po úprave a dosadení d2 = d – d1dostaneme
![]()
Potenciál je rovnaký vo vzdialenosti 12 cm od väčšieho náboja.
Príklad 8.1.10.2 Vo vrcholoch štvorca so stranami 10 cm sú umiestnené 4 rovnako veľké náboje s veľkosťou 10-7 C. Určite potenciál v strede štvorca, ak znamienka nábojov q1 , q2 , q3, q4 sú
a) ++++
b) + - + -
c) + + - -
Riešenie
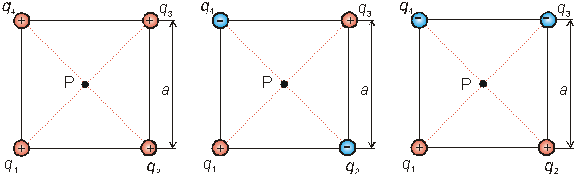
a) b) c)
Obr.8.1.11.2
Vzdialenosť vrcholu od stredu štvorca P je
![]()
.Potenciál bodového náboja v tejto vzdialenosti vypočítame podľa vzťahu
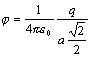 .
.
Na základe princípu superpozície elektrických polí potenciál jv bode P dostaneme ako súčet potenciálov od 4 bodových nábojov.
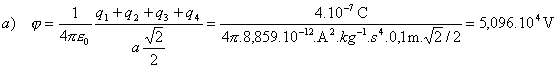
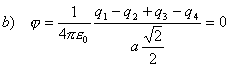
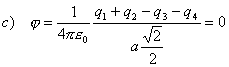
Potenciál v strede štvorca je a) 5,096.104V, b) 0V, c) 0V.
Príklad 8.1.10.3 Dve veľmi dlhé kovové valcové plochy sú súosé. Polomer vnútornej valcovej plochy je r1 , polomer vonkajšej je r2 . V priestore medzi nimi je vákuum. Na valcové plochy privedieme náboj tak, že ich pripojíme k zdroju napätia U. Po odpojení zdroja vonkajšiu plochu uzemníme. Vyšetrite potenciál elektrostatického poľa medzi plochami.
Riešenie
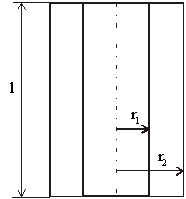
Obr. 8.1.11.3
Z Gausovej vety platí pre intenzitu poľa medzi valcovými plochami:
![]()
![]()
kde Q je náboj na vnútornej ploche, l je dĺžka valca a r je vzdialenosť od osi valca. Pritom platí r1 < r < r2 . Pre elektrostatický potenciál vo všeobecnosti platí
![]()
kde rref je polohový vektor bodu, na ktorý vzťahujeme potenciál. V našom prípade to bude uzemnená vonkajšia valcová plocha. Keďže pri výpočte potenciálu výsledná hodnota nezávisí od konkrétnej integračnej cesty, budeme ju voliť kolmo na os valca, takže v tomto prípade bude vždy E dr . Potom sa nám výpočet potenciálu zjednoduší:
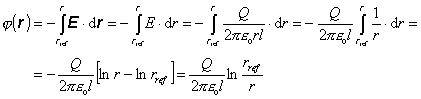
Špeciálne pre r = r1 a r = r2 dostaneme
![]()
![]()
nakoľko rref = r2 . V našom prípade je
![]()
z čoho potom
![]()
Pri známom l možno vypočítať náboj Q
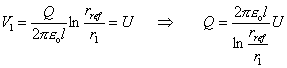
Pre potenciál vo vzdialenosti r od osi valca potom dostaneme
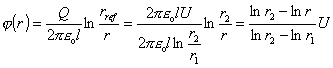
Vzťah medzi intenzitou a potenciálom elektrostatického poľa
Práca, ktorú vykonáme pri premiestnení náboja q v elektrostatickom poli E na úseku dr je
![]() (8.1.10.5.1)
(8.1.10.5.1)
Teda
![]() (8.1.10.5.2)
(8.1.10.5.2)
Elektrostatický potenciál j je vo všeobecnosti funkciou súradníc x, y, z. V I. kapitole o vektorovom počte sme ukázali, že diferenciálnu zmenu skalárnej funkcie priestorových súradníc x, y, z možno vyjadriť
![]() (8.1.10.5.3)
(8.1.10.5.3)
Porovnanie rovníc (8.1.10.5.2) a (8.1.10.5.3) ukazuje, že platí vzťah
![]() (8.1.10.5.4)
(8.1.10.5.4)
To znamená, že ak poznáme potenciál j (x, y, z), tak potom vieme v každom bode vypočítať intenzitu poľa E( x , y, z) pomocou vzťahu (8.1.10.5.4). Z rovnice (8.1.10.5.3) vyplýva, že ak vektor posunutia dr bude kolmý na gradj tak dj = 0. To znamená, že vektor posunutia dr v tomto prípade leží na ploche konštantného potenciálu j . Tým sa dostávame k dôležitému poznatku, že vektor E je v každom bode kolmý na ekvipotenciálnu hladinu, ktorá týmto bodom prechádza.
Príklad 8.1.10.4 Vychádzajúc z potenciálu j(r) bodového náboja umiestneného v začiatku súradnicového systému ukážte, že záporne vzatý grad j(r) je totožný s elektrostatickým poľom.
Riešenie
Potenciál bodového náboja q, ktorý sa nachádza v bode (0, 0, 0) je
![]() (1)
(1)
Elektrické pole v okolí tohoto náboja určíme nasledovne
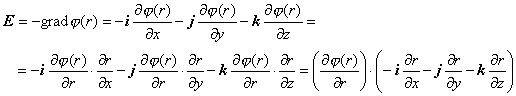
kde musíme funkciu j (r ) derivovať ako zloženú funkciu. Funkcia j je podľa rovnice (1) formálne funkciou jedinej premennej r , a preto môžeme písať
![]()
Parciálna derivácia r podľa súradnice x je
![]()
Podobne dostaneme
![]()
![]()
Teda
![]()
