Elektrické pole vo vnútri a na povrchu vodičov
Elektrické pole vo vnútri a na povrchu vodičov
|
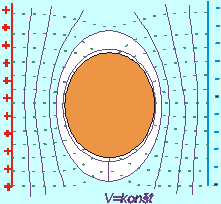
Obr. 8.2..3.1 Ekvipotenciálne plochy elektrického poľa
|
Elektrické pole, ktoré vzniklo okolo vodivého telesa vo vonkajšom elektrickom poli z predchádzajúceho príkladu, možno vyjadriť aj potenciálom. Predovšetkým si musíme uvedomiť, že každý bod vodivého telesa má rovnaký potenciál. Keďže intenzita elektrického poľa vo vodiči je nulová, aj rozdiel potenciálov ľubovoľných bodov vodivého telesa je nulový:
|
|
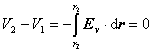
Celé teleso predstavuje jednu ekvipotenciálnu hladinu. Siločiary elektrického poľa sú kolmé na ekvipotenciálne plochy, preto intenzita elektrického poľa je na povrch vodivého telesa kolmá. Tvar ekvipotenciálnych hladín je na Obr.8.2.3.1.
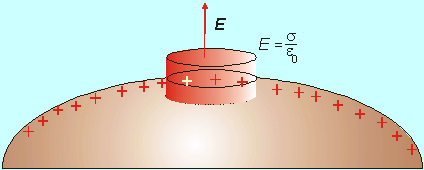
Pre elektrické pole tesne nad povrchom vodiča platí Coulombova veta: Elektrická intenzita nad povrchom vodiča je kolmá na povrch vodiča a úmerná plošnej hustote náboja. Konštanta úmernosti je prevrátená hodnota elektrickej konštanty (permitivity vákua).
![]() (8.2.3.1)
(8.2.3.1)
Pritom na zakrivených plochách je hustota náboja s nepriamoúmerná polomeru krivosti plochy R , potom teda:
Plošná hustota náboja na zakrivených plochách
|
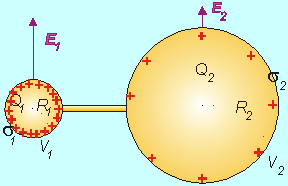
Obr. 8.2.3.3 Elektrické pole vodivého telesa s rôznym polomerom zakrivenia.
|
Náboj na povrchu vodivého telesa nemá všade rovnakú hustotu. Tá závisí od tvaru povrchu, jeho polomeru zakrivenia v danom mieste. Môžeme si to ukázať na modeli telesa zloženého z dvoch gúľ, rôzneho polomeru spojených tenkým vodivým drôtom (Obr.8.2.3.3). Takéto teleso predstavuje ekvipotenciálu hladinu, na povrchu gúľ je rovnaký potenciál. Potenciál na povrchu gule nabitej nábojom Q je rovnaký ako potenciál rovnakého bodového vo vzdialenosti R. Podľa vzťahu (8.1.10.1.3) je tento potenciál funkciou polomeru a náboja na guli a platí:
![]() , (8.2.3.6)
, (8.2.3.6)
plošná hustota náboja je nepriamoúmerná polomeru zakrivenia. Náboj sa "zhromažďuje" v miestach hrotov vystupujúcich z povrchu. Pretože intenzita poľa je úmerná hustote náboja, v takýchto miestach narastá a môže spôsobovať vytrhávanie náboja von z telesa - sršanie elektriny. Takýto elektrický výboj vo vzduchu "koróna" vzniká za normálneho tlaku, ak intenzita elektrického poľa dosiahne hodnoty 3.106 V m-1, tomu odpovedá hustota náboja 2,7.10-3 C m-2
s R = konst (8.2.3.2)![]()
Coulombova veta - odvodenie
Doteraz sme popisovali elektrické pole v nenabitých vodičoch vo vonkajších elektrických poliach. Rovnaké vlastnosti bude mať aj elektrické pole, ktoré je vytvorené nabitým vodičom. Nech na vodivom telese je náboj Q. Tento sa rozloží v telese tak, že pole vo vnútri vodiča je nulové. Preto aj náboj je rozložený len na ploche povrchu vodivého telesa. Elektrické pole na povrchu vodiča smeruje kolmo na povrch vodiča v danom mieste. Jeho veľkosť určuje tzv. Coulombova veta, ktorú odvodíme z Gaussovej vety. Zvoľme si uzatvorenú plochu, ktorú tvorí povrch malého valčeka.
|
Obr. 8.2.3.2 Odvodenie Coulombovej vety
|
Tento umiestnime do skúmaného poľa tak, že jednou podstavou leží vo vodivom telese a druhá je nad vodičom (Obr.8.2.3.2). Jeho výšku voľme veľmi malú, plochu podstavy takú malú, aby v každom jej bode intenzita poľa bola rovnaká. Potom tok intenzity elektrického poľa je nenulový len cez podstavu z vonkajšej strany telesa (vo vnútri je intenzita nulová, na stene vektor intenzity leží v ploche steny preto E . dS = 0):
![]() (8.2.3.3)
(8.2.3.3)
Náboj uzatvorený v objeme valčeka je náboj rozložený na povrchu časti plochy telesa:
![]() (8.2.3.4)
(8.2.3.4)
Po dosadení do Gaussovej vety z rovníc (8.2.3.3 a 4) intenzita na povrchu vodiča v mieste s plošnou hustotou náboja s je
![]() (8.2.3.5)
(8.2.3.5)
Coulombova veta: Elektrická intenzita nad povrchom vodiča je kolmá na povrch vodiča a úmerná plošnej hustote náboja. Konštanta úmernosti je prevrátená hodnota elektrickej konštanty (permitivity vákua).
Poznámka:
V časti 8.1.9.1, vzťah (8.1.9.1.5) bolo odvodené, že elektrická intenzita nad povrchom nekonečnej rovinnej dosky, nabitej s plošnou hustotou s je polovičná, treba to chápať tak, že aj náboj z každej "strany" roviny "na povrchu" je len polovičný.
Príklad 8.2.1 Do elektrického poľa bodového náboja Q je vložená vodivá rovinná doska veľmi veľkých rozmerov. Nakreslite tvar siločiar na oboch stranách dosky, ak doska a) nie je uzemnená, b) je uzemnená. Aké bude v týchto prípadoch rozloženie elektrického náboja na oboch povrchoch tejto dosky (kvalitatívne)?
Riešenie
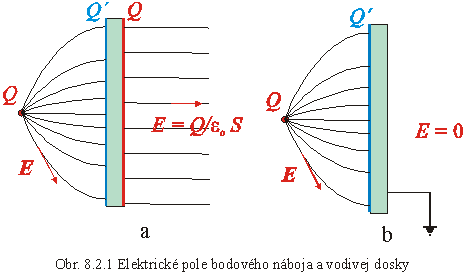
Elektrické pole, ktoré vytvára sústava bodový náboj a náboj indukovaný na doske musí mať siločiary, ktoré vychádzajú z dosky (ekvipotenciálnej hladiny) kolmo. Celkový náboj na k bodovému náboju privrátenej strane dosky je Q´ = - Q . To vyplýva zo skutočnosti, že pole vo vodivej doske je nulové. Za predpokladu nekonečnej dosky, rovina vedená stredom dosky uzatvára polpriestor s bodový nábojom, tok intenzity je nulový a preto aj celkový náboj vo vnútri Q + Q´ = 0. (V tomto priblížení aj náboj na odvrátenom povrchu dosky je nulový – nekonečná doska sa chová ako uzemnená doska, naboj – Q´ je z nej odvedený do zeme) Náboj Q´ bude od päty kolmice symetricky rozložený a pretože intenzita elektrického poľa so vzdialenosťou od bodového náboja klesá, klesať bude aj hustota náboja s rastúcou vzdialenosťou od stredu . Na druhej strane dosky bude náboj rozložený rovnomerne, za doskou sa vytvorí homogénne pole intenzity E = Q / e0S, kde S je obsah plochy dosky (Obr. 8.2.1a). v prípade, že doska je uzemnená, tento náboj sa odvedie do zeme a pole na odvrátenej strane nevznikne (Obr. 8.2.1b).
Príklad 8.2.2 Aký maximálny celkový náboj možno umiestniť na osamelej vodivej guli s polomerom R = 2 m, ak nemá dôjsť k sršaniu elektriny z hrotu umiestnenom na povrchu gule. Polomer zakrivenia hrotu je 1 cm (sršanie nastáva v mieste gule, kde intenzita poľa nad povrchom je 3.106 V m-1)
Riešenie
Elektrické pole, ktoré vytvára hrot má intenzitu prierazného napätia Em = 3.106 V m-1. Podľa Coulombovej vety je hustota elektrického náboja na hrote
sm = eoEm .
Podľa vzťahu (8.2.3.6) je hustota náboja na guli s
![]()
a celkový náboj na guli
![]()
Kontrolné otázky
- Prečo sa k prenosu elektrických signálov využíva koaxiálny kábel?
- Prečo sršanie elektriny vzniká v mieste hrotov vodivých telies?
- Na akom princípe je založený bleskozvod?
- Čo rozumieme pod pojmom dielektrikum. Je vákuum dielektrikum?
- Vysvetlite, ako sa chová dielektrikum vložené do elektrického poľa!
- Aké typy polarizácie dielektrika poznáte?
- Kolmo do homogénneho poľa vložíme rovinnú dosku. Tým sa elektrické pole zmení tak, že siločiary, ktorých hustota vyjadruje intenzitu poľa:
a) sú v doske prerušené,
b) zmenia svoju hustotu v doske oproti hustote v okolí.
O akú dosku sa jedná v prípade a) a v prípade b)