V tejto časti poukážeme na súvislosť medzi Faradayovým vzorcom 11.1.1.2 pre indukované napätie v uzavretom vodiči a vzorcom 11.1.1.5 vyjadrujúcim napätie vznikajúce medzi koncami neuzavretého vodiča, ktorý sa pohybuje v magnetickom poli.

Na obrázku 11.1.2.1 je nakreslený kúsok vodiča Dl pohybujúceho sa magnetickým poľom. Predpokladajme, že v tomto malom priestore vektor magnetickej indukcie B je konštantný, jeho smer nie je podstatný.

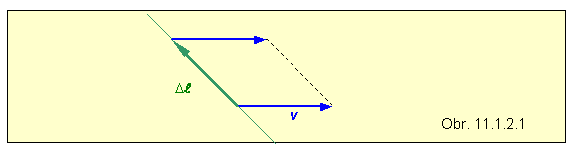
Pre indukované napätie na krátkom úseku vodiča s dĺžkou Dl , chápanom ako vektor Dl potom platí (Poznámka: editor rovníc neumožňuje napísať v rovnici Dl ako vektorovú veličinu tučným písmom):

Pri úprave sme zamenili poradie vektorov B a v a do vzťahu - do čitateľa aj do menovateľa - sme vložili krátky časový interval Dt, čím sme neovplyvnili veľkosť výsledku, ale čo umožní vzťah vhodnejšie upraviť. Pri ďalšej úprave využijeme pravidlo o zámene skalárneho a vektorového súčinu, platné pre zmiešaný súčin :

- (1/Dt) [(B x vDt) × Dl] = - B × [(vDt) x Dl] (1/Dt).

Ďalej si uvedomíme, že výraz v hranatej zátvorke [(vDt) x Dl] predstavuje vektor DS, ktorého veľkosť DS sa rovná veľkosti malej plôšky, ktorú počas krátkeho časového intervalu Dt v priestore vytvorí vektor Dl pohybujúci sa rýchlosťou v . (Na obrázku je plôška ohraničená vektorom Dl , vektormi rýchlosti v a prerušovanou úsečkou. ) . Preto môžeme písať :

- B × [(vDt) x Dl] (1/Dt) = - B × (DS / Dt ) = - D(B × S) / Dt = - DF / Dt ,

takže nakoniec dostávame výsledok

U _i = - DF / Dt ,

ktorý má zhodný tvar so vzorcom 11.1.1.2 .

Použitý postup pri získaní výsledku môže vyvolávať určité pochybnosti, napríklad v súvislosti so znamienkom mínus, vystupujúcom vo výsledku, ktoré sme získali výmenou poradia vektorov B a v . Preto uvedieme iný, exaktný postup, za cenu istého obmedzenia všeobecnosti.

Budeme uvažovať prípad uzavretého vodiča, ktorý sa vzhľadom na našu sústavu pohybuje rýchlosťou v , pričom túto rýchlosť má každý jeho element (vodič sa pri pohybe nedeformuje). Ďalej sa obmedzíme na prípad magnetického poľa, ktoré sa s časom nemení, ale v rôznych bodoch priestoru má vektor magnetickej indukcie rôzne veľkosti aj smer. Aj v tomto prípade začneme výpočet použitím vzorca 11.1.1.5, s tým rozdielom, že integrovať budeme pozdĺž celého uzavretého vodiča :

(11.1.2.1)

pričom sme na zámenu krivkového integrálu na plošný použili Stokesovu vetu. Ďalšia úprava vyžaduje podrobnejší komentár týkajúci sa výrazu rot(v x B) . Tento výraz predstavuje aplikáciu nabla operátora vektorovo na súčin funkcií. Pri aplikácii operátora by sme mali derivovať aj vektor v , ale obmedzili sme sa na prípad, že všetky elementy vodiča sa pohybujú rovnakou rýchlosťou, takže vektor v nie je funkciou priestorových súradníc. Z hľadiska derivácií predpísaných použitím operátora, je teda vektor v konštantný. Preto k operátoru nabla pripíšeme index Ñ_B , čo bude znamenať, že sa vzťahuje iba na vektor B . Preto platí:

rot(v x B) = Ñ_B x (v x B) = v (Ñ_B × B) - (v ×Ñ_B) B = v divB - v × (Ñ_BB) = - v × gradB (11.1.2.2)

lebo podľa Maxwellovej rovnice divB = 0 . Výraz v × gradB je súčasťou totálnej derivácie vektora B(x,y,z,t) podľa času :

(11.1.2.3)

Podľa predpokladu vektor B sa v žiadnom z bodov uvažovaného priestoru s časom nemení, preto jeho parciálna derivácia podľa času sa rovná nule. Potom

(dB / dt ) = v × gradB , (11.1.2.4)

a po dosadení do rovnice (11.1.2.2) dostaneme :

rot(v x B) = - (dB / dt ) . (11.1.2.5)

Posledný vzťah dosadíme do rovnice (11.1.2.1) :

(11.1.2.6)

Týmto postupom sa podarilo ukázať, že vzťahy (11.1.1.2) a (11.1.1.5) majú spoločného menovateľa. Nemožno ho však považovať za všeobecný dôkaz správnosti Faradayovho zákona elektromagnetickej indukcie.

Príklad 11.1.2.1 . V homogénnom magnetickom poli s indukciou B rotuje uhlovou rýchlosťou w vodič, ktorý má dĺžku l . Rotuje okolo svojho koncového bodu v rovine, ktorá je kolmá na vektor B , pričom vektor w je s ním súhlasne rovnobežný. Vypočítajte elektromotorické napätie, ktoré sa indukuje medzi jeho koncami a uveďte, na ktorom konci vodiča bude kladný pól el. napätia.

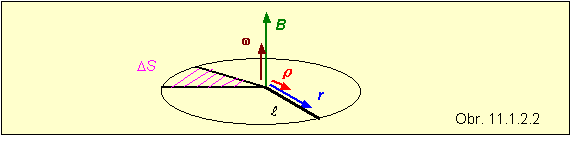
Riešenie : Príklad budeme riešiť dvojakým spôsobom.

a) Otvorený vodič (neuzavretý) sa pohybuje v magnetickom poli, takže sa v ňom indukuje intenzita el. poľa (vzorec 11.1.1.4) Ei = v x B = ( w x r ) x B , kde r = yr je polohový vektor začínajúci v strede otáčania a končiari v ľubovoľnom bode vodiča, pričom r je jednotkový vektor súhlasne rovnobežný s vektorom r . Vektor r je kolmý na vektory w a B , preto ďalšou úpravou, dostaneme :

E_i = r (w × B ) - w (r × B ) = r wB = y wB r ,

z čoho vyplýva, že vektor E_i je súhlasne rovnobežný s vektorom r . Preto elektróny, nesúce záporný elektrický náboj, sa budú pohybovať proti intenzite, t.j. k stredu otáčania, ktorý bude predstavovať záporný pól. Veľkosť el. napätia získame integráciou intenzity od stredu otáčania po okraj vodiča :

b) Rovnaký výsledok dostaneme, ak použijeme vzorec 11.1.1.2 , pričom zmenu magnetického toku získame vynásobením magnetickej indukcie prírastkom plochy DS (na obrázku je vyšrafovaná), ktorú opíše otáčajúci sa vodič za jednotku času, resp. obsahom kruhu vydeleným periódou otáčania :

Ui = ( pl²B ) / (T ) = ( pl²B ) / (2p /w) = (1/2) w B l² .

Príklad 11.1.2.2 . V homogénnom magnetickom poli s magnetickou indukciou B sa konštantnou uhlovou rýchlosťou w otáča pravouhlý závit s rozmermi a, b . Otáča sa okolo svojej osi symetrie, ktorá je kolmá na vektor B . Vypočítajte, aké elektromotorické napätie sa indukuje v závite, a akú má maximálnu hodnotu.

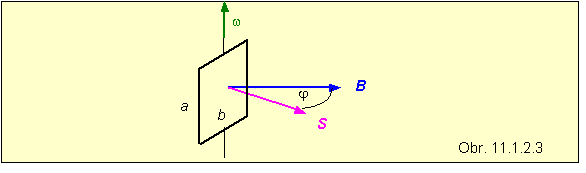
Riešenie Použijeme vzorec 11.1.1.2 Ui = - (dF/dt) , pričom magnetický tok vyjadríme ako skalárny súčin F = B × S = B S cos j . Uhol j sa s časom mení, pričom platí j = w t , takže aj magnetický tok cez plochu ohraničenú závitom sa mení : F = B S cos( w t ) . Indukované napätie dostaneme deriváciou magnetického toku :

U_i = - (dF/dt) = + BS w sin (w t) = U_max sin (w t) .

Výpočtom sme získali hneď aj maximálne indukované napätie : U_max = BS w = Bab w .

Poznámka: Uvedený príklad 11.1.2.2 reprezentuje princíp vzniku striedavého sínusového napätia, aké sa generuje v alternátoroch.

 

Kontrolné otázky

1. Jestvuje súvislosť medzi Faradayovým vzorcom pre indukované napätie a vzorcom pre napätie medzi koncami vodiča pohybujúceho sa magnetickým poľom ?
2. Z hľadiska indukovaného napätia - vedie zmena magnetického toku uzavretým vodičom k rovnakým výsledkom ako jeho pohyb nehomogénnym magnetickým poľom ?
3. Môže otáčaním priameho vodiča v magnetickom poli vzniknúť medzi jeho koncami rozdiel el. potenciálov ?
4. Môže otáčanie uzavretého vodiča v homogénnom magnetickom zapríčiniť pohyb elektrického náboja v ňom ?
5. Akú polohu musí mať os otáčania kruhového závitu vzhľadom na rovinu závitu a vzhľadom na vonkajšie magnetické pole, aby sa v ňom indukovalo najväčšie napätie ?
6. Môže v uzavretom vodiči, otáčajúcom sa v homogénnom magnetickom poli jedným smerom, vzniknúť striedavé napätie ?