 Geometrická optika
Geometrická optika
Vlnová podstata svetla vnáša do optiky mnoho problémov. Ak používame optické elementy, ktorých vlastné rozmery sú v porovnaní s použitou vlnovou dĺžkou veľké, možno vlnové vlastnosti svetla zanedbať. Aproximácia v ktorej zanedbávame vplyv vlnových vlastností sa nazýva geometrická optika.
Použitím jednoduchých geometrických pravidiel môžeme v rámci aproximácie veľkých optických elementov študovať činnosť optických prístrojov. Na obrázku sú nakreslené svetelné lúče pri zobrazovaní predmetu na rovinnom zrkadle (A) a na jednoduchej lupe (B).
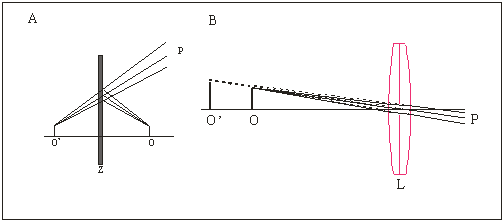
V oboch prípadoch pozorovaný objekt O „vysiela“ svetelné lúče, ktoré sa odrážajú na zrkadle, alebo lámu na lupe. Zdanlivý objekt O’ vzniká v bode kde sa zdanlivé lúče pretínajú. Zdanlivý objekt môže byť rovnako veľký ako skutočný (zrkadlo), alebo zväčšený (lupa).
Príkladom zložitejšieho optického prístroja je mikroskop (obrázok dole). Skladá sa z objektívu a okulára. Pozorovaný objekt O je umiestnený pred objektívom.
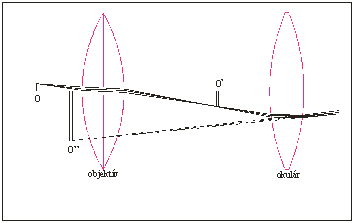
Medzi objektívom a okulárom vzniká skutočný obraz O’ – pretínajú sa skutočné lúče. Zdanlivý obraz O“ vzniká pred objektívom a je zväčšený.
Ohnisková vzdialenosť guľovej plochy
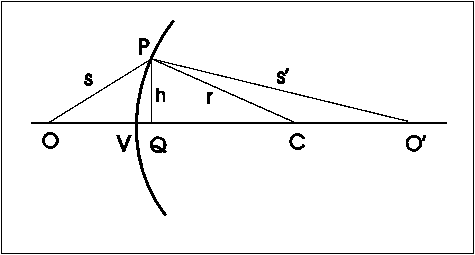
Predpokladajme, že guľová plocha oddeľuje dve prostredia s rôznymi indexmi lomu, tak ako je to zobrazené v obrázku:
Predpokladáme, že vľavo sa index lomu rovná jednej a vpravo nejakej hodnote n>1. V tomto prostredí sa svetlo šíri pomalšie o faktor n. Skutočná rýchlosť svetla vpravo od guľovej plochy teda je:
v=c/n (4.1.1)
Nech je v bode O umiestnený zdroj svetla, ktorý vysiela svetelný lúč smerom k guľovej ploche po dráhe OP. Vo vzdialenosti s´ v pravej časti je umiestnený bod O´. Zakrivený povrch plochy treba upraviť tak, aby lúč vychádzajúci z bodu O sa na povrchu guľovej plochy ohol tak, aby dopadol do bodu O´ bez ohľadu na polohu bodu P na povrchu guľoplochy. Výpočet vo všeobecnosti vedie na určenie plochy štvrtého rádu a nie je to ľahké spočítať ani vyrobiť . V špeciálnom prípade, ak lúč prichádza z nekonečna, je riešenie jednoduchšie a úlohu možno vyriešiť pomocou plochy druhého rádu – paraboly. Keďže primeraný povrch nie je jednoduché vyrobiť, obvykle sa uchýlime ku kompromisu a povrch tvarujeme tak, aby bol rovný guľovej ploche. V takomto prípade ohyb lúčov nie je nezávislý na polohe bodu P a v bode O´ sa stretnú len tie lúče, ktoré sú vyžiarené z bodu O pod malým uhlom.
Teraz sme už pripravený odvodiť všeobecnú rovnicu, ktorá bude opisovať vlastnosti guľoplochy. Za predpokladu, že bod P sa nachádza blízko priamky OO´ (osi), urobíme z bodu P kolmicu na os, ktorej výšku označíme ako h. Predstavme si, že pozdĺž úsečky PQ prechádza rovina, ktorá ohraničuje prechod medzi prostrediami. V takom prípade by čas, ktorý potrebuje lúč na prechod z bodu O do P bol väčší ako čas potrebný na prechod medzi bodmi OQ. Rovnako by to bolo v prostredí s indexom lomu n (vpravo). Z tohto dôvodu musí byť povrch zakrivený, aby svojim tvarom kompenzoval časové rozdiely tak, aby, ktorý prechádza po dlhšej dráhe absolvoval väčšiu časť dráhy v „rýchlejšom“ prostredí. Nadbytočný čas po dráhe OP sa rovná
Dt1= h2/(2s) (4.1.2)
a nadbytočný čas po zbytku dráhy PO´ sa rovná
Dt2=h2/(2s´) (4.1.3)
Tento nadbytočný čas, ktorý sa musí vyrovnať oneskoreniu pozdĺž dráhy VQ, sa líši od času, ktorý by platil pre vákuum, pretože je tu iné optické prostredie. Keďže rýchlosť svetla v prostredí s indexom lomu n je pomalšia o faktor n, oneskorenie na tejto vzdialenosti je potom (n-1)VQ. Ak je polomer guľovej plochy r, vzdialenosť d medzi bodmi VQ je rovná
d(VQ) = h2/(2r) (4.1.4)
Na základe jednoduchých geometrických úvah sme objavili vzťah medzi vzdialenosťami s a s´, ktorý určuje hľadaný polomer krivosti guľovej plochy r:
![]() (4.1.5)
(4.1.5)
alebo po jednoduchej úprave
![]() (4.1.6)
(4.1.6)
Ak máme danú polohu bodu O a polohu druhého bodu O´ a chceme sústrediť svetlo z bodu O do bodu O´ tak polomer guľovej plochy možno vypočítať pomocou vzťahu (4.1.6). Pre určitú guľoplochu s definovaným polomerom zakrivenia a indexom lomu n, potom platí, že
![]() (4.1.7)
(4.1.7)
Zo vzťahu (4.2.7) vidno, že ak budeme zväčšovať vzdialenosť s, vzdialenosť s´ sa bude zmenšovať. V hraničnom prípade, ak s posunieme do nekonečna budú sa všetky lúče pretínať v polovične vzdialenosti polomeru krivosti guľovej plochy. Tento bod nazveme ohniskom guľovej plochy (označujeme ho ako F) a vzdialenosť Vf nazývame ohniskovou vzdialenosťou f. Pomocou tejto vzdialenosti, ktorá sa určí ľahšie ako polomer krivosti guľovej plochy, možno vzťah (4.2.6) prepísať do tvaru, ktorý sa bežne používa:
![]() (4.1.8)
(4.1.8)
Predchádzajúce tvrdenia odporúčame potvrdiť pomocou interaktívneho obrázku v úvode časti Geometrická optika.
Ohnisková vzdialenosť šošovky
Šošovka je tvorená dvomi povrchmi (vo všeobecnosti) s rôznymi krivosťami povrchu. Priestor medzi nimi je vyplnený sklom, prípadne iným materiálom s dostatočne vysokým indexom lomu, ktorý označíme n.
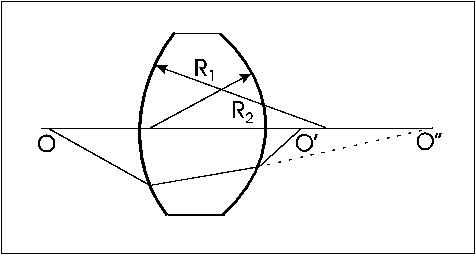
Na tejto sústave chceme študovať problém prechodu svetelného lúča z bodu O do bodu O´. Na začiatku sa to môže zdať zložité, ale dá sa to urobiť celkom jednoducho. Najskôr použijeme vzťah (4.1.5) pre prvý povrch a zabudneme na ten druhý. Ten nám povie, že svetlo sa bude zbiehať v bode O“. Na dráhe lúča bude ležať nový povrch oddeľujúci sklo a vzduch. Znovu použijeme ten istý vzťah a ten nám povie že lúč sa v skutočnosti dostane do bodu O´. Tento postup možno použiť na ľubovolný počet povrchov. Samozrejme existujú veľmi presné (a zložité) vzťahy, ktoré umožňujú riešiť tento problém priamo, ale predchádzajúci postup je dostatočne účinný a možno ho s výhodou použiť pri počítačovej simulácii.
Výpočet prechodu lúča cez dva zakrivené povrchy možno zjednodušiť v prípade ak sú tieto povrchy dostatočne blízko seba a možno zanedbať chyby súvisiace s hrúbkou.
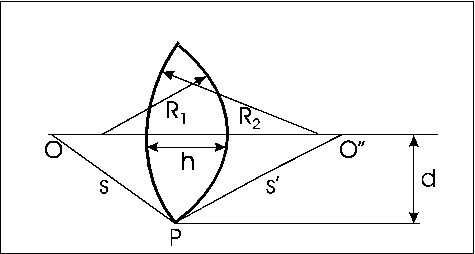
Predpokladajme, že lúč prechádzajúci z bodu O do bodu O´ dopadá presne na hranu šošovky. Potom oneskorenie na dráhe lúča je dané:
![]() (4.2.1)
(4.2.1)
pričom sme zanedbali prítomnosť šošovky hrúbky h vyplnenej sklom s indexom lomu n. Aby sa čas potrebný k prechodu lúča po dráhe OPO“ rovnal času prechodu lúča po priamej dráhe musíme tomuto vložiť do cesty kúsok skla hrúbky h s indexom lomu n tak aby sa oneskorenie lomeného lúča vyrovnalo. Preto hrúbka šošovky v strede musí byť daná vzťahom:
![]() (4.2.2)
(4.2.2)
Hrúbku šošovky v strede možno vyjadriť pomocou polomerov krivostí povrchov nasledovne:
![]() (4.2.3)
(4.2.3)
Spojením vzťahov (4.2.2) a (4.2.3) dostaneme výsledný vzťah:
![]() (4.2.4)
(4.2.4)
Keď sa bod O nachádza v nekonečne, bod O“ sa bude nachádzať v bode, ktorý nazveme ohnisková vzdialenosť šošovky f. Hodnotu tejto vzdialenosti vypočítame pomocou vzťahu:
![]() (4.2.5)
(4.2.5)
Ak nepoznáme polomery krivosti, možno ohniskovú vzdialenosť šošovky „odmerať“ pomocou vzdialeností s a s´ pomocou vzťahu:
![]() (4.2.6)
(4.2.6)
Zväčšenie
V tejto časti sa budeme zaoberať polohou bodov ležiacich mimo optickej osi a ich zobrazeniu za šošovkou. Pre lepšie pochopenie si predstavme sústavu svietiacich bodov, ležiacich na jednej úsečke. Za šošovkou uvidíme, že lúče z týchto bodov sa sústreďujú znovu do bodov ležiacich na inej úsečke, ktorá je väčších / menších rozmerov. Schematicky je to zobrazené na obrázku (použili sme symetrickú tenkú šošovku, ktorú na obrázku znázorňuje priamka QT):
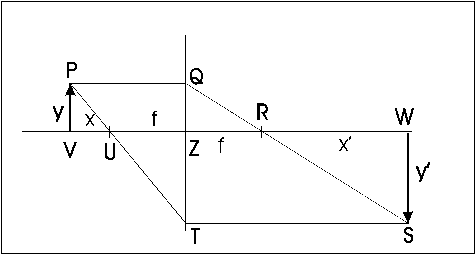
Z predchádzajúcich častí poznáme tieto pravidlá geometrickej optiky:
- Lúč vchádzajúci na jednej strane do šošovky rovnobežne s osou, sa láme tak že na druhej strane prechádza ohniskom šošovky.
- Lúč prechádzajúci ohniskom šošovky na jednej strane sa po prechode šošovkou láme tak, že smeruje rovnobežne s osou na druhej strane.
Tieto dve (jednoduché) pravidlá nám umožňujú vypočítať polohu a veľkosť zobrazenej úsečky. Svietiacu úsečku sme nahradili šípkou výšky y. Jej vzdialenosť od ohniska označme x. Jeden z lúčov, ktoré vychádzajú z jej konca P je nasmerovaný v smere PQ pozdĺž osi. Tento sa ohne tak, že prechádza ohniskom ( bod R) na druhej strane. Ak sa bod P zobrazí na druhej strane, bude to na priesečníku najmenej dvoch lúčov. Treba teda nájsť trajektóriu ešte aspoň jedeného lúča. Takým je lúč vychádzajúci z bodu P , ktorý prechádza ohniskom (bod U) na jednej strane a láme sa rovnobežne na druhej strane. Obidva lúče sa pretínajú v bode S, ktorý tvorí vrchol zobrazovanej úsečky SW. Výšku zobrazenej úsečky označme y´ a jej vzdialenosť od ohniska x´. Použitím vlastností podobných trojuholníkov PVU a TZU môžeme napísať rovnosť:
![]() (4.3.1)
(4.3.1)
Podobne použitím trojuholníkov QZR a RSW dostaneme rovnosť:
![]() (4.3.2)
(4.3.2)
Porovnaním výšok objektov (podielov y´/y) dostaneme:
![]() (4.3.3)
(4.3.3)
čo je známa šošovková rovnica. Obsahuje všetko čo potrebujeme o šošovkách vedieť. Možno pomocou nej spočítať zväčšenie šošovky a tiež dáva do súvisu vzdialenosti x a x´ s ohniskovou vzdialenosťou f.
![]() (4.3.4)
(4.3.4)
Tieto jednoduché pravidlá umožňujú napísať program na zobrazenie geometrických zväčšení.
Pri pokusoch s interaktívnym obrázkom možno ukázať, ze v prípade ak sa objekt nachádza v kratšej vzdialenosti od šošovky, ako je ohnisková vzdialenosť obraz nevzniká za šošovkou ale pred šošovkou. Takýto obraz nazývame virtuálny.
Aberácia
Pri jednoduchej geometrickej interpretácii vlastnosti šošovky sme sa obmedzili len na lúče ležiace blízko optickej osi (paraxiálne lúče) respektíve sme vlastnosti paraxiálnych lúčov použili aj na lúče ležiace ďaleko od optickej osi. Reálna šošovka nemá takéto „dobré“ vlastnosti. Lúč ležiaci „ďaleko“ osi nebude prechádzať presne ohniskom, ale bude sa od neho vzďaľovať. Výsledkom bude, že vzdialenejší bod sa bude zobrazovať nie ako bod, ale ako malá škvrnka. Tento jav sa nazýva sférická aberácia. Dá sa odstrániť tak, že namiesto sférického (guľového) tvaru použijeme iný (zložitejší) tvar šošovky.
Šošovky majú ešte inú chybu ktorá vzniká v dôsledku toho že rýchlosť svetla v skle závisí od frekvencie. Teda aj poloha ohniska sa mení v závislosti od frekvencie svetla. Ak napríklad chceme zobraziť kombináciu modrej a červenej farby vychádzajúcej z jedného bodu, výsledkom bude, že tieto dva body budú navzájom posunuté. Táto chyba sa nazýva chromatická aberácia. Chyba chromatickej aberácie sa dá odstrániť kombinovaním šošoviek vyrobených z rozličného skla.
Rozlišovacia schopnosť
Štúdiom vlastností geometrickej optiky možno nadobudnúť dojem, že vhodnou kombináciou šošoviek možno dosiahnuť ľubovolné zväčšenie optického zariadenia. Ako uvidíme nie je to možné. Pravidlo, ktoré určuje ako ďaleko musia byť od seba dva body, aby sa ich obraz javil tiež ako dva body, sa dá sformulovať pomocou času, ktorý lúče z rozličných bodov potrebujú na cestu optickým systémom.
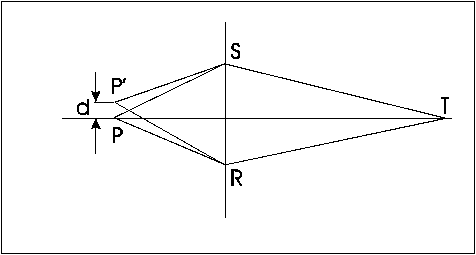
Predpokladajme že z bodu P ležiaceho na osi prejdú všetky lúče do bodu T za rovnaký čas. To nie je celkom pravda – vďaka aberácii, ale tento fakt nebudeme v našom odvodení brať do úvahy. Teraz zoberme iný bod P´ ležiaci blízko bodu P. Podľa princípov geometrickej optiky by sa tento mal zobrazovať v blízkosti bodu T a teda vždy ich možno odlíšiť. V skutočnosti je to zložitejšie – body môžu byť vďaka nedokonalosti systému rozmazané. Podmienkou, aby sa dali odlíšiť je to, aby prvý bod bol zaostrený na odlíšiteľne inom mieste ako druhý bod. Do dosiahneme, ak sa časy po dráhach P´ST a P´RT nerovnajú, pretože v prípade rovnosti časov by sa bod P´ zobrazoval na osi. Zostáva odpovedať na otázku o koľko sa musia časy líšiť, aby vznikol obraz mimo osi. Všeobecné pravidlo optiky hovorí, že dva rozdielne bodové zdroje sa dajú rozlíšiť vtedy, keď jeden zdroj sa zobrazí do takého bodu, že čas potrebný pre okrajové lúče vychádzajúce z druhého zdroja do toho bodu sa v porovnaní s jeho skutočným obrazovým bodom líši o viac ako o jednu periódu. Je teda potrebné, aby časový rozdiel medzi horným a dolným lúčom do nepravého bodu obrazu bol väčší ako perióda kmitov svetla. Dôsledok tohto tvrdenia je, že so skracujúcou sa vlnovou dĺžkou (teda s narastajúcou frekvenciou) bude rásť rozlišujúca schopnosť sústavy.
