 Rayleighov-Jeansov zákon vyžarovania
Rayleighov-Jeansov zákon vyžarovania
Problém spektra dokonale čierneho telesa riešili koncom 19. storočia na základe klasickej predstavy, že tepelné žiarenie má pôvod v zrýchlenom pohybe častíc v blízkosti povrchu telesa, ktoré pôsobia ako malé antény (oscilátory). Žiarenie v dutine dokonale čierneho telesa, s dokonale odrážajúcimi stenami o teplote T, uvažovali ako rad stojatých elektromagnetických vĺn.
V podstate išlo o trojrozmerné zovšeobecnenie stojatého vlnenia napnutej struny. Podmienka pre vznik stojatého vlnenia v dutine vyžaduje, aby dĺžka dráhy od steny k stene v ľubovoľnom smere bola celočíselným násobkom polovice vlnovej dĺžky. To znamená, že na každej odrazovej ploche bude uzol. Pre kocku o hrane L podmienkou pre vznik stojatého vlnenia v smer osi x, y, resp. z bude
![]()
![]()
![]()
V prípade, že jx = jy = jz pre stojatú vlnu v ľubovoľnom smere musí platiť
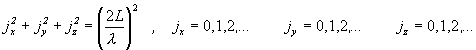
aby vlna mala uzly na obidvoch svojich koncoch. K určeniu počtu stojatých vĺn n(l) dl v jednotkovom objeme dutiny, ktorých vlnové dĺžky ležia medzi l a l + d l, musíme určiť počet dovolených trojíc jx, jy a jz , ktoré dávajú vlnové dĺžky z tohto intervalu a predeliť ich objemom dutiny L3. K tomuto výpočtu si zavedieme j-priestor, ktorého pravouhlé súradnicové osi tvoria jx, jy a jz . V takto zvolenej súradnicovej sústave každý bod j-priestoru odpovedá dovolenej trojici čísel jx, jy , jz a teda i stojatej vlne. Vzdialenosť bodu daného súradnicami jx, jy, jz od počiatku sústavy určuje veľkosť vektora j.
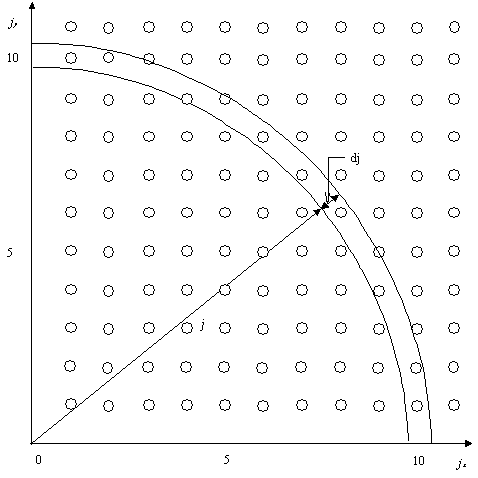
Celkový počet vlnových dĺžok z intervalu l a l+ d l sa rovná počtu bodov nachádzajúcich sa v j-priestore, ktorých vzdialenosť od počiatku je medzi j a j + d j. Uvažujeme len tú časť guľového priestoru, kde hodnoty jx, jy , jz sú kladné. Objem tejto časti gule o polomere j a hrúbke dj je 4p j2 dj / 8. Keďže pre j a diferenciál dj nám platí
![]() ,
,
![]()
vidíme, že zväčšeniu vlnovej dĺžky l odpovedá zmenšenie j.
Pre celkový počet dovolených vlnových dĺžok N (l)dl v dutine dostaneme
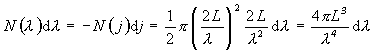 .
.
Objem dutiny tvaru kocky o hrane L je L3, takže pre počet stojatých vĺn v jednotkovom objeme
n (l) d![]() = N (l)dl/ L3
= N (l)dl/ L3
Pri zvážení dvoch navzájom kolmých smerov polarizácie každej stojatej vlny, skutočný počet nezávislých stojatých vĺn v dutine je dvojnásobný, t.j.
![]() (1)
(1)
Rayleigh na určenie strednej energie stojatej vlny využil poznatok, že stredná hodnota energie lineárneho harmonického oscilátora je určená súčinom kT, t.j. Boltzmannovej konštanty a absolútnej teploty:
Poznámka: Táto skutočnosť vyplýva z ekvipartičnej teorémy, podľa ktorej stredná energia pripadajúca na jeden stupeň voľnosti objektu, ktorý je v tepelnej rovnováhe pri teplote T je kT/2 , kde k je Boltzmanova konštanta. Lineárny oscilátor má jeden stupeň voľnosti. Zvyšnú kT/2 dostaneme z potenciálnej energie z teorémy o viriále.
V našom prípade pôvodcom každej vlny je atómový oscilátor, ktorý má dva stupne voľnosti, odpovedajúce kinetickej a potenciálnej energii. Každá stojatá vlna má strednú energiu
![]() = kT
= kT
a teda spektrálna hustota intenzity vyžarovania Ml (l,T) dl jednotkového objemu dutiny v intervale vlnových dĺžok l al + d l je Ml(l,T)dl =e n(l)dl=kTn(l)dl, resp. vyjadrená vzťahom (13.1.2.5)
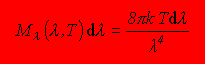
Získaný vzťah sa nazýva Rayleighov a Jeansov zákon vyžarovania pre absolútne čierneho teleso.
Z jeho rozboru vyplýva:
· pre veľké vlnové dĺžky l ® ¥ nám predpovedá pokles intenzity, s ktorou sa energia vyžaruje k nule, čo súhlasí s experimentálnymi pozorovaniami;
· pre malé vlnové dĺžky l ® 0 predpovedá nárast intenzity, s ktorou sa energia vyžaruje do nekonečna, čo sa vžilo pod názvom tzv. ultrafialová katastrofa, ktorá je v rozpore s experimentom.
Skutočnosť:
· Pozorovania však ukázali, že s poklesom vlnových dĺžok k ultrafialovej oblasti intenzita žiarenia klesá až k nulovej hodnote.
Ktorý z predpokladov použitých pri odvodzovaní bol nesprávny?
· Z hľadiska klasickej fyziky boli všetky správne a vychádzali z predpokladu, že ekvipartičný teorém platí len pre spojité rozdelenie energií, avšak ako Max Planck ukázal energia elektromagnetickej vlny s kmitočtom f je v skutočnosti kvantovaná v jednotkách hf.
