 De Broglieho vlna
De Broglieho vlna
Experimenty, diskutované v úvodnej časti tejto kapitoly (13.1.1 až 13.1.4) boli vysvetlené na základe nových myšlienok Maxa Plancka, Alberta Einsteina a tiež Arthura Comptona. Nové prístupy prispeli k uzavretiu sporu medzi správnosťou dvoch teórií –vlnovou a časticovou podstatou svetla. Všetky majú spoločný rys, že vlneniu prisúdili energiu a hybnosť na základe korpuskulárnej predstavy vlnenia ako toku častíc.
Tieto experimenty prezentovali, že vlnenie má aj látkové vlastnosti. Po rokoch nejednotnosti a váhania, ktorá z teórií bola správna, bolo možno spor uzavrieť konštatovaním, že obidve strany mali pravdu. Fotón je „častica“ i „vlna“ zároveň. Za istých okolností sa prejavuje svojimi vlnovými vlastnosťami (ohyb, interferencia) a za iných okolností prejavuje korpuskulárne (časticové) vlastnosti (Comptonov jav, fotoefekt,..) Doteraz sa predpokladalo, že fotón nemôže vykazovať obidve vlastnosti súčasne. V súčasnosti sa ukazuje, že to tak nie je. Môže mať obe vlastnosti súčasne.
Takáto vlastnosť vlno-častice sa odrazila v novom formalizme nevyhnutnom pri odvodení jej pohybovej rovnice, zavedení neurčitosti a nemožnosti všetko si predstaviť a zdôvodniť v kvantovej fyzike. Jednými z „nepochopiteľných“ skutočností boli i Bohrove postuláty (paragraf 13.2.2). Napriek tomu, že Bohrovi sa podarilo vysvetliť vodíkové emisné spektrá, v rokoch 1913-1926 mala táto teória veľa odporcov. Medzi nich sa radil i Albert Einstein. Hlavným argumentom bol vysoký počet postulátov, t.j. tvrdení bez dôkazov. Ukážeme si, že prevratná myšlienka Louisa de Broglieho iným spôsobom potvrdí druhý Bohrov postulát.
Louis de Broglie (1892 –1987) vychádzal zo známych poznatkov symetrie v prírode a preto túto symetriu hľadal i v prípade súboru častíc. Ak je pravdou, že elektromagnetické vlnenie sa prejavuje duálnym charakterom, prečo by sa obdobný charakter nemohol pripustiť i pre hmotné telesá. Ak zväzok svetla, prezentovaný ako vlna, môže odovzdávať energiu a hybnosť hmote v kvantách – fotónoch, prečo by sa nemohlo zväzku pohybujúcich sa elektrónov, resp. ľubovolnej pohybujúcej sa častici, prisúdiť vlnu hmoty. Svoju teóriu zverejnil L. de Broglie v roku 1924, v ktorej navrhol, že nielen fotónu, ale i každej pohybujúcej sa hmotnej častici s hybnosťou o veľkosti p, možno prisúdiť vlnenie s vlnovou dĺžkou l, určenou vzťahom

Vlnová dĺžka l určená rovnicou 13.3.2.1, kde v je rýchlosť pohybujúcej sa častice a m je hmotnosť častice, sa nazýva de Broglieho vlnová dĺžka. V relativistickej fyzike možno hmotnosť m vyjadriť cez pokojovú hmotnosť m0 častice danej vzťahom
 (13.3.2.2)
(13.3.2.2)
kde c je rýchlosť svetla vo vákuu. Rovnicu (13.3.2.1možno inprpretoať:
Každej pohybujúcej sa častici s konštantnou energiou E a hybnosťou p, t.j. konajúcej rovnomerný priamočiary pohyb, prislúcha rovinná vlna s frekvenciou f a vlnovým vektorom k, ktoré sú určené vzťahmi:
k = (2p/l)n = 2p p/h, (13.3.2.3)
f = E/h, (13.3.2.4)
kde n je jednotkový vektor v smere šírenia sa vlny, t.j. v smere rýchlosti v .
Teória L. de Broglieho bola prvýkrát experimentálne potvrdená o tri roky neskôr (1927) C. J. Davisonom a L. H. Germerom z Bellových laboratórií a tiež P. Thomsonom. V roku 1989 bola vlnová povaha elektrónu demonštrovaná i na pokuse s difrakciou na dvoch štrbinách (obr. 13.3.1.3), diskutovaným v časti 13.3.1.

Otázka na zamyslenie sa: Ak pripustíme, že elektrón má duálne vlastnosti, obdobne ako fotón a pri svojom pohybe okolo jadra sa šíri vo forme bližšie neurčenej vlny; možno nájsť nejakú súvislosť Bohrovej kvantovacej podmienky, určenej rovnicou (13.2.2.4) s Comptonovou hypotézou? Odpoveď znie áno a o akú súvislosť sa jedná ukáže nasledovný postup:
Vyjadrime Bohrovu kvantovú podmienku v tvare
![]() ,
,
kde pn určuje veľkosť hybnosti elektrónu na n-tej orbite. Ak dosadíme za hybnosť z rovnice (13.3.2.1), dostaneme
![]()
Rovnica (13.3.2.5) vyjadruje skutočnosť, že obvod dovolenej dráhy, po ktorej sa elektrón pohybuje je celočíselným násobkom vlnovej dĺžky prináležiacej vlne pohybujúceho sa elektrónu. K tomu aby nedochádzalo k interferenčným javom a následnému zániku vlno-častice, musí sa na obvod orbitálnej dráhy (orbitu) „zmestiť" celistvý počet vĺn, ako je to schematicky naznačené na obr. 13.3.2.1. Teda nutnou podmienkou vytvorenia stacionárneho stavu na n-tej orbite s polomerom rn je podmienka
![]() , (13.3.2.5)
, (13.3.2.5)
kde l je vlnová dĺžka hypotetickej vlny, prislúchajúcej obiehajúcemu elektrónu, vyjadrujúca stabilný stav pri vzniku stojatého vlnenia, kde n = 1, 2, …
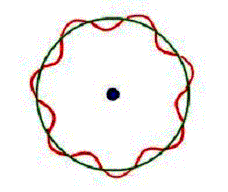
Obr. 13.3.2.1 Schématické znázornenie stojatej vlny na stacionárnej dráhe atómu vodíka
V prípade ak by obvod dráhy nebol celočíselným násobkom, dochádza k interferencii vlnenia a k vytvoreniu nestacionárneho stavu. Podmienka (13.3.2.5) vyjadruje súvislosť Comptonovej vlnovej dĺžky s vytvorením stojatého vlnenia na n-tej orbite a je taktiež vyjadrením podmienky stabilných dráh elektrónov v atóme vodíka.
Príklad 13.3.2.1 Na základe de Broglieho teórie priraďte elektrónu na prvej kvantovej dráhe v atóme vodíka vlnovú dĺžku a pojednajte o interpretácii kvantovej Bohrovej podmienky .
Riešenie Z Bohrovej kvantovej podmienky si vyjadrime hybnosť elektrónu
![]() (1)
(1)
Po dosadení za hybnosť z rovnice 13.3.2.1 a vzťahu medzi redukovanou a Planckovou konštantou, pre vlnovú dĺžku na n-tej orbite dostaneme vzťah
![]() (2)
(2)
Pre elektrón, pohybujúci sa na prvej kvantovej dráhe, t.j. po dosadení Bohrovho polomeru r1 = 5.3.10-11 m a
n = 1 , dostávame vlnovú dĺžku
l1= 33.10-11 m
Rovnicu (2) , ktorá je ekvivalentná rovnici (13.3.2.5)
2p rn = n l, ,
možno interpretovať dvomi spôsobmi :
q Elektrón môže krúžiť okolo jadra bez vyžarovania nekonečne dlho za predpokladu, že jeho dráha obsahuje celočíselný počet de Broglieho vĺn.
q Elektrón sa bez vyžarovania nachádza na stabilných orbitách, t.j. na tých dráhach (orbitách), ktorých obvod sa rovná celočíselnému počtu de Broglieho vĺn.
Príklad 13.3.2.2 Určite vlnovú dĺžku prislúchajúcu elektrónu urýchlenému v elektrickom poli s potenciálnym rozdielom U = 100 V. Porovnaním vlnových dĺžok zatrieďte priradenú „hmotnostnú“ vlnu do elektromagnetického spektra.
Riešenie Pohyb elektrónu možno popisovať nerelativisticky, keďže pre jeho rýchlosť bude platiť v << c, kde c je rýchlosť svetla. Elektrón urýchľovaný v elektrostatickom poli, získa kinetickú energiu, ktorá sa rovná práci poľa, teda platí
![]() .
.
Ak uvážime vzťah 13.3.2.1, po dosadení jednotlivých hodnôt pre de Broglieho vlnovú dĺžku dostaneme
![]()
Príklad 13.3.2.3 Vypočítajte de Broglieho vlnovú dĺžku elektrónu s pokojovou hmotnosťou m0 = 9,1.10-31 kg, pohybujúceho sa rýchlosťou v = 0,8 c.
Riešenie Vychádzame zo vzťahu (13.3.2.1) pre de Broglieho vlnovú dĺžku, pričom berieme do úvahy relativistický nárast hmotnosti daný vzťahom (13.3.2.2)
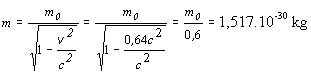 .
.
Vlnová dĺžka potom je
![]() .
.
Poznámka: Dozvedeli sme sa niečo o vlne pravdepodobnosti a o vlno-častici. Nedá mi na tomto mieste neuviesť zaujímavú myšlienku Tomáša Akvinského, z roku 1268, o ktorú sa s nami podelil náš kolega a priateľ doc. RNDr. Peter Ballo, PhD.:
Anjel môže postupne opúšťať miesto, na ktorom bol skôr, deliteľne, a tak jeho pohyb bude súvislý.
Môže zároveň opustiť celé miesto a objaviť sa naraz v celku na druhom mieste, a tak jeho pohyb bude nesúvislý.
A tak anjel v jednom okamžiku môže byť na jednom mieste a v inom okamžiku na inom mieste, bez toho aby bol nejaký čas v mieste prostrednom.
(Tomáš Akvinský 1268)
Kontrolné otázky
- Vyslovte základnú myšlienku de Broglieho hypotézy?
- Napíšte vzťah vyjadrujúci závislosť vlnového vektora od smeru šírenia sa vlnenia.
- Pri pohybe častice s rýchlosťou v <<c , kde c je rýchlosť svetla, vyjadrite de Broglieho vlnovú dĺžku ako funkciu kinetickej energie .
- Existuje súvislosť medzi Bohrovou kvantovou podmienkou a de Broglieho vlnovou dĺžkou? Ak áno, vyslovte ju a matematicky zapíšte.
- Vysvetlite pojem stacionárnej dráhy elektrónu v atóme vodíka z pohľadu de Broglieho teórie.
- Koľko vlnových dĺžok sa zmestí na dráhu, prebehnutú elektrónom na tretej kvantovej dráhe?
- Napíšte rovnicu, ktorá uvádza súvis medzi hmotnosťou a energiou.
- Vysvetlite pojem vlnovo-korpuskulárneho dualizmu.
- Ktoré experimenty podporujú vlnovú teóriu svetla?
- Ktoré experimenty podporujú korpuskulárnu povahu svetla?
- Ktorú myšlienku zovšeobecnil Louise de Broglie pri formovaní de Broglieho hypetézy?
