 Vektorová funkcia
Vektorová funkcia
Základnými charakteristikami vektorových veličín sú ich veľkosť a smer. Tieto charakteristiky môžu závisieť od času, prípadne od priestorových súradníc, podobne ako pri skalárnych veličinách. Napríklad teplota vo vybranom bode v miestnosti sa môže meniť s plynúcim časom, ráno je iná ako popoludní. V tomto prípade ide o skalárnu funkciu jednej premennej - času. Vo väčšej miestnosti však v rovnakom čase nemusí byť teplota v rôznych miestach rovnaká. V takom prípade ide o skalárnu funkciu priestorových súradníc. Z tohto pohľadu najvšeobecnejšia skalárna funkcia závisí od času, aj od priestorových premenných. Podobné závislosti sú možné aj pri vektorových veličinách. Napríklad rýchlosť prúdenia vody v rieke v pevne zvolenom bode koryta vo všeobecnosti sa s časom mení, závisí od vodného stavu. A istotne v danom časovom okamihu v rôznych miestach rieky je rýchlosť rôzna - nie iba čo do veľkosti, ale aj čo do smeru.
Preto možno hovoriť o vektorových funkciách viacerých premenných, špeciálne priestorových súradníc x, y, z a času t . Túto skutočnosť vyjadrujeme zápisom f (x,y,z,t) . Každá vektorová funkcia má v trojrozmernom priestore vo všeobecnosti tri zložky, pričom každá zložka opäť závisí od priestorových, aj od časovej súradnice. Preto funkciu f pomocou zložiek zapíšeme v tvare
f (x,y,z,t) = fx (x,y,z,t) i + fy (x,y,z,t) j + fz (x,y,z,t) k (1.3.1.1)
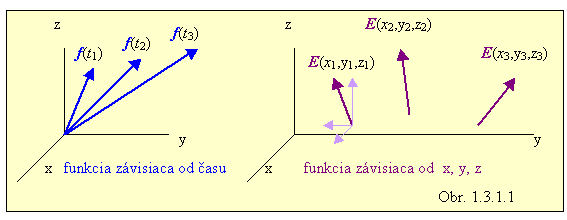
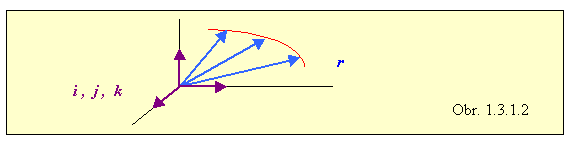
Špeciálnym prípadom je vektorová funkcia, ktorá závisí len od času : f(t) (obr.1.3.1.1 vľavo). Je to funkcia, pri ktorej s plynúcim časom sa vo všeobecnosti mení jej veľkosť i smer. V súlade s vyjadrením podľa (1.3.1.1) má tri zložky, pričom vo zvolenej súradnicovej sústave každá z jej súradníc závisí od času, nie však od priestorových súradníc. Vhodným príkladom je polohový vektor pohybujúcej sa častice r(t) , ktorý spája začiatok súradnicovej sústavy s časticou, takže koniec vektora sa posúva po krivke, po ktorej sa častica pohybuje (obr. 1.3.1.2) :
r (t) = x(t) i + y (t) j + z(t) k
Príkladom vektorovej funkcie závisiacej od priestorových súradníc, ale nemeniacej sa s časom, je vektor intenzity E v elektrostatickom poli bodového náboja. Túto jeho závislosť vyjadrujeme zápisom E (x,y,z) . Znázornená je na obr. 1.3.1.1 vpravo.
Pri opise fyzikálnych dejov, alebo polí, nestačí poznať len hodnoty funkcií, ale aj ich zmeny, či už súvisiace s plynúcim časom, alebo zmeny pozdĺž jednotlivých priestorových súradníc. Na tento účel slúžia derivácie vektorových funkcií. Opačnou matematickou operáciou je integrácia vektorovej funkcie, ktorou získavame spravidla rozdiely hodnôt funkcií, alebo hodnoty týkajúce sa istého objemu (objemový integrál), ohraničenej plochy (plošný integrál), alebo časti krivky (krivkový integrál). Vo všetkých prípadoch je pojem vektorovej funkcie, ktorá závisí od priestorových súradníc, rozhodujúci.
Kontrolné otázky
-
Uveďte z praxe príklad skalárnej funkcie závisiacej od času !
-
Uveďte príklad skalárnej funkcie závisiacej od priestorových súradníc !
-
Uveďte príklad vektorovej funkcie závisiacej iba od času !
-
Uveďte príklad vektorovej funkcia závisiacej od priestorových premenných a času !
