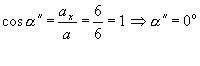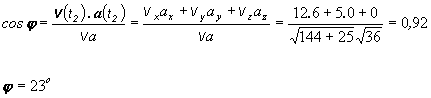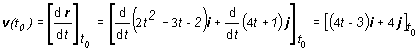Zrýchlenie
Zrýchlenie
Definícia zrýchlenia je analogická ako pri rýchlosti. Zrýchlenie zavádzame ako deriváciu vektora rýchlosti podľa času, teda ako vektorovú veličinu, ktorá určuje veľkosť, aj smer zmeny vektora rýchlosti:
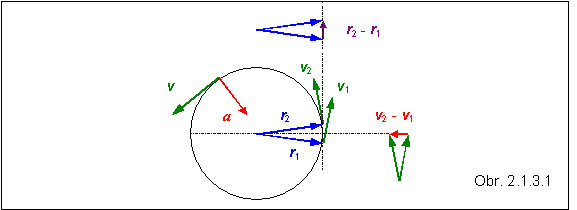
Keďže vektor rýchlosti je prvou deriváciou polohového vektora, vektor zrýchlenia je súčasne druhou deriváciou polohového vektora. Vektor zrýchlenia vo všeobecnosti nemá smer vektora rýchlosti. Napríklad pri pohybe častice po kružnici, ak sa veľkosť jej rýchlosti nemení, mení sa neustále smer vektora rýchlosti, a teda častica má zrýchlenie, ktoré ako vektor, je na vektor rýchlosti v každom okamihu kolmé. Toto si možno overiť na obr. 2.1.3.1, ak si uvedomíme, že časové okamihy t1 a t2 sa v limite k sebe približujú. Zatiaľ čo rozdiel vektorov r2 - r1 v limite má smer dotyčnice kružnice, teda smer kolmý na polohový vektor, vektor v2 - v1 je v limite kolmý na vektor rýchlosti, teda kolmý na dotyčnicu kružnice.
Podobne ako pri rýchlosti, aj pri zrýchlení platia vzťahy :
kde h je jednotkový vektor vyjadrujúci smer vektora zrýchlenia. Jednotkou zrýchlenia je m/s2 , pretože ide o druhú deriváciu polohového vektora podľa času.
Príklad 2.1.3.1
Hmotný bod sa pohybuje tak, že jeho polohový vektor závisí na čase podľa vzťahu r(t) =A t3 i +Bt j +Ck, kde A = 1 m.s –3, B = 5 m.s-1, C = -3 m. Určite:
a) vektory r, v, a v okamihu t1= 1 s výpočtom a graficky ;b) veľkosti r, v , a v okamihu t1= 1 s ;c) smerové uhly r, v , a v okamihu t1= 1 s ;d) uhol j, ktorý zvierajú vektor rýchlosti v a vektor zrýchlenia a v okamihu t2= 2 s ;
Riešenie
a) r(t) =A t3 i +Bt j +Ck = t3 i +5 t j -3 k,
r(t1) = i +5 j -3 k, [m],
v (t1) = 3 i + 5 j [m.s-1]
b)c) smerové kosínusy a smerové uhly polohového vektora r (t1):smerové kosínusy a smerové uhly vektora rýchlosti v(t1):smerové kosínusy a smerové uhly vektora zrýchlenia a(t1):d) uhol vektorov rýchlosti a zrýchlenia v časovom okamihu t2 = 2 sUrčime vektor rýchlosti v danom okamihu: v(t2) = 3.4 i + 5 j a vektor zrýchlenia v danom okamihu: a(t2) = 6 i . Ich uhol možno vypočítať použitím skalárneho súčinu.
Príklad 2.1.3.2
Polohový vektor pohybujúcej sa častice je v SI sústave určený vzťahom r(t)= (At2-Bt-C)i+(Dt+1)j, kde A =2 m.s-2, B = 3 m.s-1, C = 2 m, D = 4 m.s-1.Určite
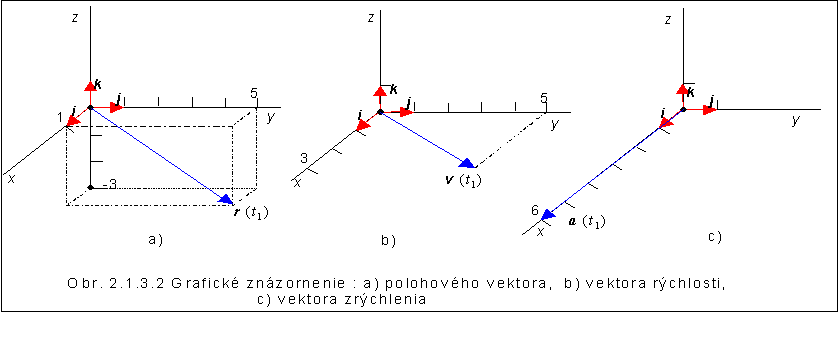
a) veľkosť vektorov r, v a a na začiatku pohybu, t.j. t0 = 0;b) graficky znázornite vektory r, v a a na začiatku pohybu;c) časový okamih t 1, v ktorom vektor rýchlosti je rovnobežný s osou y.
Riešenie
Keďže z-tová súradnica častice je nulová, častica sa pohybuje v rovine xy.
a) r(t0)= (2.0-3.0-2)i +(4.0+1) j = 2 i +jv (t0)= -3 i +4 j [m.s-1]veľkosť a (t0) = 4 [m.s-2]b)
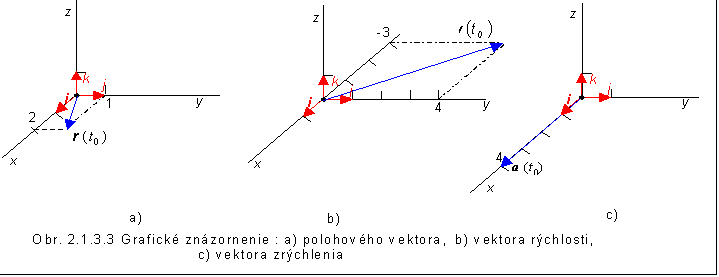
c) Vektor rýchlosti je určený predpisom v (t)= (4 t –3)i + 4j. Ak má byť vektor rovnobežný s osou y, jeho x-ová zložka musí byť nulová, t.j. v x (t1)= 4 t1 - 3 = 0 Þ t1 = 3/4 s.
Kontrolné otázky
-
Vyslovte definíciu zrýchlenia.
-
Matematicky formulujte definíciu zrýchlenia .
-
Formulujte dve závislosti zrýchlenia ako funkciu času.
-
Napíšte vzťah pre zrýchlenie v zložkovom tvare. Ako možno vyjadriť jednotlivé zložky zrýchlenia?
-
Napíšte vzťah pre veľkosť zrýchlenia.
-
Aký smer vo všeobecnosti má vektor zrýchlenia?
-
Môže nastať prípad, keď vektor rýchlosti a zrýchlenia majú rovnaký smer? Ak áno, uveďte príklad.
-
Napíšte jednotku zrýchlenia v sústave SI.
-
Napíšte smerové kosínusy vektora zrýchlenia.