Dokonale tuhé teleso je teleso, ktoré sa pôsobením síl nedeformuje, t. j. vzdialenosti medzi jeho jednotlivými časťami sa zachovávajú. Jeho objemová hmotnosť r je daná podielom hmotnosti veľmi malej časti objemu a tohoto objemu:

 

Hmotný stred je totožný s ťažiskom telesa, ktoré je definované ako pôsobisko tiažovej sily v homogénnom tiažovom poli pri ľubovolnom otočení telesa

Polohový vektor hmotného stredu je daný vzťahom:

 

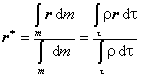
Translačný (posuvný) pohyb telesa je pohyb, pre ktorý rýchlosti všetkých bodov telesa sú v každom okamihu rovnaké; všetky body telesa sa pohybujú po trajektóriach, ktorých tvar je rovnaký, sú len posunuté v priestore, podľa voľby bodu telesa.

Rotačný (otáčavý) pohyb telesa je pohyb, v ktorom každý bod telesa vykonáva pohyb po kružnici a stredy týchto kružníc ležia na jednej priamke, ktorú voláme os rotácie

 

V dokonale tuhom telese možno urobiť redukciu síl. Pôsobenie sústavy teleso je ekvivalentné pôsobeniu výslednej sily rovnajúcej sa vektorovému súčtu týchto síl pôsobiacej v zvolenom bode a súčasnému pôsobeniu momentu sily rovnajúcemu sa vektorovému súčtu momentov pôvodných síl vzhľadom na ten istý zvolený bod.

 

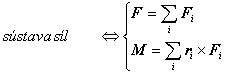
Prvá pohybová rovnica pre dokonale tuhé teleso vyjadruje skutočnosť, že: časová zmena celkovej hybnosti tuhého telesa sa rovná výslednici vonkajších síl.

kde hybnosť telesa: je definovaná

,

 

Veta o pohybe hmotného stredu (ťažiska) vyjadruje skutočnosť, že časová zmena hybnosti hmotného stredu sa rovná výslednici vonkajších síl, hmotný stred sa pohybuje tak, ako keby v ňom bola sústredená celá hmotnosť a pôsobila naň výslednica vonkajších síl

kde hybnosť hmotného stredu:

je rýchlosť hmotného stredu

 

Druhá pohybová rovnica pre dokonale tuhé teleso vyjadruje skutočnosť, že časová zmena celkového momentu hybnosti sa rovná výslednici momentu vonkajších síl vzhľadom na ten istý momentový bod.

časová zmena celkového momentu hybnosti sa rovná výslednici momentu vonkajších síl vzhľadom na ten istý momentový bod.

Integráciou cez časový interval dostávame tzv. impulzové vety.

kde moment hybnosti tuhého telesa:

,

vzťažný bod pre moment síl a moment hybnosti je rovnaký, je začiatok polohového vektora r, ktorý určuje polohu hmotného elementu dm pohybujúceho sa rýchlosťou v.

Integrálnym tvarom pohybových rovníc sú impulzové vety. Prvá impulzová veta:

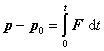
kde p, p₀ sú celkové hybnosti telesa na konci resp. začiatku časového intervalu.

Druhá impulzová veta

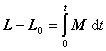
kde L a L_o sú celkové momenty hybnosti telesa na konci resp. začiatku časového intervalu.

 

Podmienky rovnováhy tuhého telesa sú: súčet všetkých vonkajších síl a súčet všetkých momentov týchto síl vzhľadom na jeden ľubovoľne zvolený momentový bod je nulový vektor, sú vyjadrené vzťahmi:

 

Pohybová rovnica pre otáčanie telesa okolo pevnej osi vyjadruje skutočnosť, že moment sily vzhľadom na os sa rovná súčinu momentu zotrvačnosti telesa vzhľadom na túto os a uhlového zrýchlenia

kde moment sily vzhľadom na os je vektorová veličina daná priemetom momentu sily vzhľadom na bod, ktorý je na osi otáčania, do osi otáčania

a moment zotrvačnosti je mierou zotrvačných vlastností rotujúceho telesa.

kde r je kolmá vzdialenosť hmotného elementu od danej osi a

Steinerova veta

Moment zotrvačnosti J vzhľadom na ľubovoľnú os sa rovná momentu zotrvačnosti J^* vzhľadom na os, ktorá je s ňou rovnobežná a prechádza hmotným stredom, zväčšenému o moment zotrvačnosti hmotného bodu o hmotnosti m rovnajúcej sa hmotnosti telesa a nachádzajúceho sa vo vzdialenosti a rovnej vzájomnej vzdialenosti osí.

 

Kinetickú energiu telesa hmotnosti m pohybujúceho sa translačnou rýchlosťou v^* a rotačnou rýchlosťou w vyjadruje vzťah

kde je moment zotrvačnosti telesa vzhľadom na os prechádzajúcu hmotným stredom.

V izolovanej sústave platí zákon zachovania mechanickej energie, napr. v tiažovom poli Zeme:

 

Pohybová rovnica fyzikálneho kyvadla hmotnosti m, ktoré je zavesené na vodorovnej osi vo vzdialenosti a hmotného stredu od osi, a ktorého moment zotrvačnosti vzhľdom na os otáčania je J je

.

Riešením pre malá výchylky j je harmonická funkcia