 Príklady
Príklady
Príklad 1
Dva voľné hmotné body A a B s hmotnosťami m1 a m2 sú v rovnomernom pohybe. V čase t = 0 je vzdialenosť bodov AB = d. Rýchlosť v2 bodu B má smer spojnice AB a rýchlosť v1 bodu A je na ňu kolmá. Nájdite rovnicu dráhy a rýchlosť ťažiska tejto sústavy hmotných bodov. Aký pohyb vykonáva ťažisko?
Riešenie
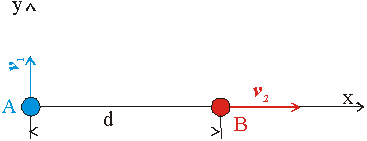
Súradnice ťažiska sú
Vylúčime čas t, čo znamená, že z rovnice pre x-ovu súradnicu ťažiska vyjadríme čas t a dosadíme do rovnice pre y-ovu súradnicu. Po úprave dostaneme
čo je rovnica priamky.
Nájdeme rýchlosť ťažiska. Z definície
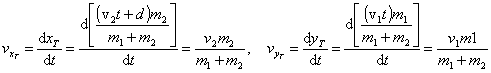
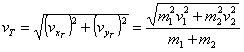
Príklad 2
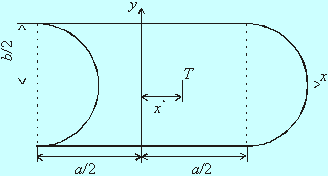
Nájdite polohu ťažiska útvaru znázorneného na obr.1, ktorý vznikol tak, že sa z obdĺžnika so stranami a, b vyrezal na jednej jeho strane polkruh polomeru b/2 a priložil sa na druhú stranu obdĺžnika!
Riešenie
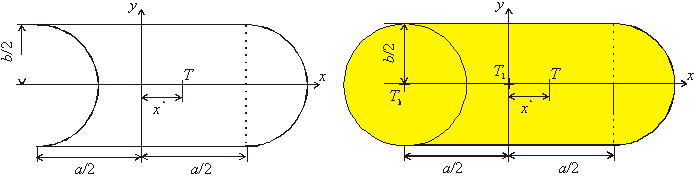
Ak k nášmu útvaru (obr.1) priložíme kruh, dostaneme žltý útvar, ktorý je znázornený na obr.2. T je ťažisko nášho útvaru, Tk je ťažisko kruhu, T1 je ťažisko žltého útvaru.
x-ová súradnica ťažiska žltého útvaru je
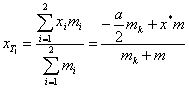 (1)
(1) kde mk je hmotnosť kruhu, m je hmotnosť nášho útvaru, x* je x-ová súradnica ťažiska nášho útvaru.
Nech σ je plošná hustota (hmotnosť pripadajúca na jednotku plochy), potom
m= σ ab
dosadíme do rovnice (1), uvážime, že xT1=0 a dostaneme
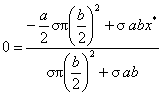
po úprave vypočítame x-ovú súradnicu ťažiska, ktorá je
Príklad 3
Vypočítajte moment zotrvačnosti tenkého drôtu hmotnosti m zohnutého do tvaru kružnice polomeru R vzhľadom na os kolmú na rovinu, v ktorej leží kružnica a prechádzajúcu stredom kružnice.
Riešenie
Príklad 4
Vypočítajte moment zotrvačnoti homogénnej tyče prierezu S0, dĺžky l a hmotnosti m vzhľadom na os kolmú na dĺžku tyče a prechádzajúcu a) koncovým bodom tyče, b) ťažiskom tyče!
Riešenie
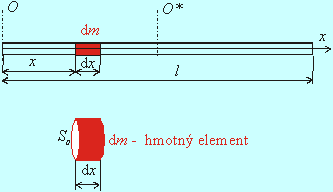
Riešenie a)
Pre moment zotrvačnosti tyče vzhľadom na os O (obr.1) možno písať
kde hmotný element dm je valec, ktorého podstava je So a výška je dx (obr.1)
Nech ρ je hustota tyče (hmotnosť pripadajúca na jednotku objemu), potom hmotný element
dosadíme do rovnice (1) a dostaneme
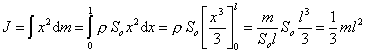
hustotu ρ sme vyjadrili v tvare
Riešenie b)
Pri riešení využijeme Steinerovu vetu
kde J* je moment zotrvačnosti tyče vzhľadom na os O* prechádzajúcou stredom tyče, teda ťažiskom. Z rovnice (2) vyjadríme
Príklad 5
Vypočítajte moment zotrvačnosti homogénneho plného valca hmotnosti m , polomeru R, výšky h vzhľadom na rotačnú os totožnú s jeho osou symetrie. Zvážte, od čoho nezávisí.
Riešenie
J = 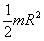 .
.
Príklad 6
Tenký drôt hmotnosti m je zohnutý do tvaru kružnice polomeru R a uložený v tiažovom poli na vodorovnú os. Po malom vychýlení z rovnovážnej polohy ho voľne pustíme. Vypočítajte dobu kyvu a redukovanú dĺžku tohto kyvadla !(Riešte pre hodnoty R=4,9cm, g = 9,8 m.s-2).Riešenie
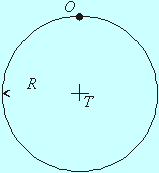
Drôt predstavuje fyzikálne kyvadlo. Pre dobu kyvu fyzikálneho kyvadla platí
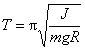 (1)
(1)Moment zotrvačnosti drôtu vzhľadom na os prechádzajúcu ťažiskom je
Podľa Steinerovej vety je moment zotrvačnosti vzhľadom na os O (obr.1) nasledovný
Po dosadení do rovnice (1) dostaneme
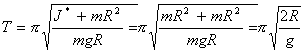
Dĺžka matematického kyvadla, ktorého doba kyvu Tmat sa rovná dobe kyvu fyzikálneho kyvadla Tfyz sa nazýva redukovaná dĺžka lr. Pre uvedené doby kyvu platí
Z rovnosti rovníc (2) a (3) dostaneme
a odtiaľ
Príklad 7
Zotrvačníkové koleso, ktoré má spolu s hriadeľom moment zotrvačnosti vzhľadom na os otáčania J, otáča sa tak, že vykonáva N otáčok za minútu. V okamihu, keď prestanú pôsobiť vonkajšie sily svojím otáčavým momentom, koleso sa zastaví počas doby tz. Za predpokladu, že trecie sily sú konštantné, vypočítajte ich moment vzhľadom na os! (Riešte pre hodnoty 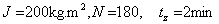 )
)
Riešenie
Trecie sily sú konštantné, preto sa koleso bude otáčať rovnomerne spomalene, pre takýto pohyb platí
ω= ωo-ε t (1)
Vypočítame uhlové spomalenie ε. V čase zastavenia tz sa uhlová rýchlosť ω=0, dosadíme do rovnice (1), dostaneme
0= ωo-ε tz,
odtiaľ
Moment síl trenia vzhľadom na os Mν vypočítame z pohybovej rovnice rotácie telesa okolo pevnej osi
Mν=J ε (3)
Po dosadení (2) do (3) dostaneme
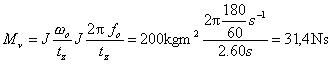
Príklad 8
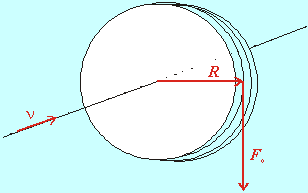
Homogénna kruhová doska je uložená na vodorovnej osi prechádzajúcej jej stredom a kolmej na rovinu dosky. Na obvode je navinuté lanko, ktoré ťaháme silou Fo kolmou na os, v dôsledku čoho sa dá doska do otáčavého pohybu. Vypočítajte uhlovú rýchlosť a kinetickú energiu dosky po čase t od začiatku pôsobenia sily ! Hmotnosť dosky je m a polomer R. (Riešte pre hodnoty m = 20 kg, R = 0,5 m, t = 2 s, Fo =9.81N)Riešenie
Pohybová rovnica telesa rotujúceho okolo pevnej osi je
Mν=J ε. (1)
Moment sily vzhľadom na os Mν vypočítame z definície
význam vektorov je zakreslený na obr.1,
veľkosť momentu sily v našom prípade je
Mν=RFo (2)
Pohyb je rovnomerne zrýchlený, preto platí
ω= ε t (3)
Rovnicu (1) možno zapísať
odtiaľ
využili sme poznatok, že moment zotrvačnosti kruhovej dosky okolo osi kolmej na dosku a prechádzajúcej jej ťažiskom je
Teleso koná rotačný pohyb, jeho kinetická energia je
Príklad 9
Homogénna tyč všade rovnakého prierezu, hmotnosti m, dĺžky l voľne visí na vodorovnej osi prechádzajúcej jej koncovým bodom O. Akú minimálnu rýchlosť treba udeliť voľnému koncovému bodu tyče v horizontálnom smere, aby sa dostala do najvyššej možnej polohy ? (Trenie zanedbávame.) (Riešte pre hodnoty l = 1 m, m = 2,5 kg !)Riešenie
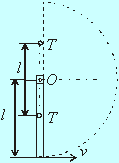
Obr.1
Tyč koná rotačný pohyb.
Úlohu riešime zákonom zachovania mechanickej energie.
Energiu tyče v dolnej polohe označme Wd, energiu v hornej polohe Wh.
Platí
Wd=Wh (1)
Energia v dolnej polohe je
kde J je moment zotrvačnosti tyče vzhľadom na os O (obr.1), potenciálnu energiu v ťažisku sme volili rovnú nule.
Energia v hornej polohe je
kinetická energia je nulová, lebo teleso stojí, potenciálna energia sa rovná zmene potenciálnej energie ťažiska.
Dosadíme do rovnice (1)
kde J=1/3 ml2 (pozri príklad č.4), ω = v/l. Dosadíme do rovnice (2), po úprave dostaneme
Príklad 10
Valec sa valí po naklonenej rovine, ktorá zviera s vodorovnou rovinou uhol α. Polomer valca je R a hmotnosť m. a) Vypočítajte rýchosť jeho ťažiska v* po prebehnutí dráhy s, keď valec bol voľne pustený. Polomer valca je R a hmotnosť m. b) Porovnajte vypočítanú hodnotu s rýchlosťou, ktorú by malo ťažisko, keby sa valec len šmýkal po dokonale hladkej podložke.
Riešenie
a) 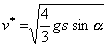
b) 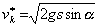
Príklad 11
Vypočítajte kinetickú energiu homogénnej gule rotujúcej okolo priemeru s konštantným uhlovým zrýchlením e v čase t od začiatku pohybu ! Hmotnosť gule je m a polomer R.( Riešte pre hodnoty 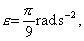 t = 10 s, m = 1,5 kg, R = 5 cm )
t = 10 s, m = 1,5 kg, R = 5 cm )
Riešenie
Príklad 12
Homogénna kruhová doska polomeru R sa nachádza vo vertikálnej rovine a môže sa otáčať okolo vodorovnej osi kolmej na dosku a vzdialenej od stredu dosky x. Dosku vychýlime z rovnovážnej polohy do polohy, v ktorej je stred dosky vo výške osi a potom ju voľne pustíme. Vypočítajtea) začiatočné uhlové zrýchlenie dosky
b) uhlovú rýchlosť pri prechode rovnovážnou polohou
(Trenie na osi zanedbávajte !)
Riešenie
