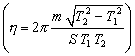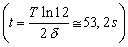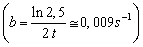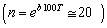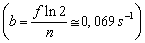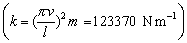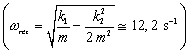Vynútený kmitavý pohyb
Vynútený kmitavý pohyb
Pod vynúteným kmitaním rozumieme pohyb, ktorý nastane, ak na kmitajúcu sústavu okrem návratnej sily a odporu prostredia pôsobí periodická nútiaca sila. Príklad takejto sústavy je zobrazený na obrázku 6.1.10.
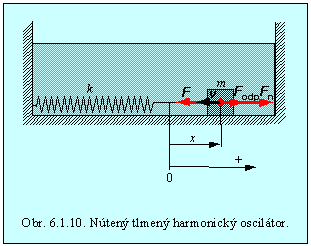
Nech časová závislosť nútiacej sily je Fn = F0 cos(Wt), kde F0 je amplitúda nútiacej sily a W je jej kruhová frekvencia. Výslednica síl pôsobiacich na hmotný bod hmotnosti m je
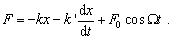 (6.1.7.1)
(6.1.7.1)Pohybová rovnica má tvar
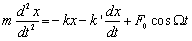 (6.1.7.2)
(6.1.7.2)Prepíšeme ju do tvaru
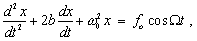 (6.1.7.3)
(6.1.7.3)kde f0 = F0/m a b a w0 majú rovnaký význam, ako pri tlmenom kmitavom pohybe. Od rovnice (6.1.6.2) sa táto rovnica líši tým, že pravá strana sa nerovná nule. V matematike sa dokazuje, že všeobecné riešenie tejto rovnice je súčtom riešenia rovnice bez pravej strany, čo je práve funkcia pre tlmené kmity a partikulárneho integrálu pravej strany rovnice (6.1.7.3). Z teórie diferenciálnych rovníc platí
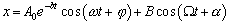 (6.1.7.4)
(6.1.7.4)Prvý člen riešenia s časom exponenciálne zaniká, preto stacionárne riešenie predstavuje druhý člen rovnice (6.1.7.4) a dostávame
Ak teda vonkajšia nútiaca sila pôsobí dostatočne dlhý čas, sústava začne kmitať s frekvenciou rovnajúcou sa frekvencii nútiacej sily. Toto sme mohli očakávať aj na základe fyzikálnej intuície a skúsiť či takéto riešenie rovnici (6.1.7.3) bude vyhovovať. Konštanty B a a v riešení (6.1.7.5) nemôžu mať ľubovoľnú hodnotu, musia byť také, aby vyhovovali pohybovej rovnici nútených kmitov. Nájdime najprv amplitúdu vynútených kmitov.
Dosaďme riešenie (6.1.7.5.) do rovnice (6.1.7.3). Dostávame
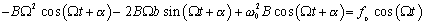 (6.1.7.6)
(6.1.7.6)Táto rovnica bude mať najjednoduchší tvar pri takých hodnotách času t, kedy sa cos(Wt + a) bude rovnať 1 alebo 0, teda Wt + a = 0, resp. Wt + a = p/2.
Po dosadení takýchto fáz dostávame
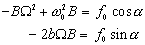
Umocnením týchto rovníc, sčítaním a úpravou dostávame rovnicu pre amplitúdu vynútených kmitov
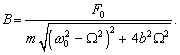 (6.1.7.7)
(6.1.7.7)Vidíme, že amplitúda vynútených kmitov bude za inak rovnakých podmienok závisieť od uhlovej frekvencie nútiacej sily. Kmity s maximálnou amplitúdou nazývame rezonančné kmity a frekvencia pri ktorej dochádza k takýmto kmitom je rezonančná frekvencia amplitúdy. Rezonančnú frekvenciu určíme z podmienky extrému funkcie B(W). Rezonancia nastane, keď táto amplitúda bude maximálna. Hľadáme extrém funkcie B = B(W), t.j. splnenie podmienky
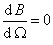
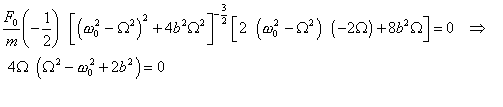
Pre rezonančnú frekvenciu dostávame:
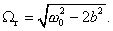 (6.1.7.8)
(6.1.7.8)Priebeh amplitúdy v závislosti od frekvencie nútiacej sily je na obr. 6.1.11.
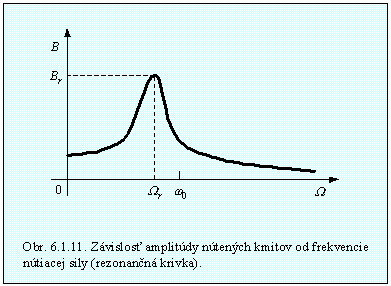
Pri vynútenom kmitaní pôsobí odpor prostredia a dochádza k disipácii energie. Mechanická energia sa mení na iné formy energie. napr. teplo. Pri ustálenom stave je amplitúda kmitov a teda aj celková mechanická energia konštantná a podľa (6.1.3.2) sa rovná
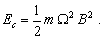
Straty mechanickej energie v dôsledku odporu prostredia |Fodp| = k’v sa kompenzujú energiou dodávanou sústave vonkajším zdrojom nútiacej sily. Za rovnováhy sa bude výkon nútiacej sily potrebný na kompenzáciu disipovanej energie rovnať P = Fodp v = k’v2. Pre rýchlosť platí
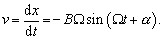
Rýchlosť sa periodicky mení a jej amplitúda je
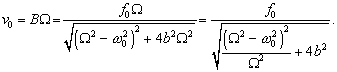
Výkon nútiacej sily bude závisieť od frekvencie nútiacej sily. Bude maximálny pri maximálnej hodnote amplitúdy rýchlosti. Tá ako vidíme z predchádzajúceho vzťahu, bude maximálna ak bude menovateľ čo najmenší, z čoho vyplýva podmienka pre rezonanciu energie.
Rezonancia energie nastáva pri frekvencii
Rezonancia energie nastáva pri frekvencii
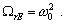 (6.1.7.9)
(6.1.7.9)Pri tejto frekvencii vonkajšej nútiacej sily zdroj nútiacej sily odovzdáva za jednotku času maximálnu energiu. Rezonančná frekvencia pre energiu nezávisí na veľkosti tlmenia.
V praxi sa často stretávame s rezonančnými javmi. Na rezonancii v elektrických obvodoch, je založená napríklad prakticky celá rádiokomunikácia. Ak ladíme rádioprijímač, tak iba prispôsobujeme prijímací obvod rádioprijímača frekvencii daného vysielača. Rezonančná absorbcia energie má veľký význam pri určovaní štruktúry molekúl. Ak sú molekuly umiestnené do premenlivého elektrického poľa a niektorá z vlastných frekvencií vibrácii atómov v molekule (vibrácii väzieb) je v rezonancii s meniacim sa vonkajším elektrickým poľom výrazne sa zvýši pre túto frekvenciu absorbcia energie, čo sa dá využiť pri určovaní štruktúry molekúl.
Rezonancia sa využíva tiež v niektorých mechanických meracích prístrojoch. Mechanické rezonancie však môžu mať aj veľké negatívne účinky. Napríklad len pôsobením malej sily môže dôjsť k takým veľkým amplitúdam kmitov, že sa poruší pevnosť materiálov, hriadeľov, mostov a pod. a dôjde k ich deštrukcii.
Príklad 6.1.16
Kmitavá sústava koná tlmené kmity s frekvenciou f = 1000 Hz. Vypočítajte frekvenciu vlastných kmitov sústavy fo, keď rezonančná frekvencia pre amplitúdu sústavy je fr = 998 Hz.
Riešenie
Pre uhlovú frekvenciu tlmených kmitov platí:
kde b je koeficient tlmenia a ω0 je uhlová frekvencia netlmených kmitov. Pri vynútených kmitoch za rezonancie platí podmienka:
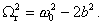
Úpravou týchto dvoch rovníc dostaneme:
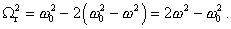
Odtiaľ uhlová frekvencia vlastných kmitov sústavy je:
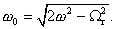
Pretože pre frekvencie platí ω0 = 2p f0, ω = 2p f, Wr = 2p fr, hľadaná frekvencia vlastných kmitov sústavy bude:
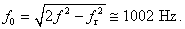
Príklad 6.1.17
Teleso hmotnosti m = 0,1 kg zavesené na pružine s koeficientom tuhosti k1 = 10 N.m–1 koná vynútené harmonické kmity v odporujúcom prostredí s koeficientom odporu k2 = 0,8 kg.s–1. Vypočítajte koeficient tlmenia, uhlovú frekvenciu vlastných kmitov, rezonančnú amplitúdu a rezonančnú uhlovú frekvenciu, keď amplitúda nútiacej sily Fo = 1.10–1 N.
Riešenie
Pohybová rovnica vynútených kmitov má tvar:
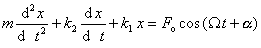
Pre koeficient tlmenia b platí:
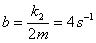
Pre uhlovú frekvenciu vlastných kmitov platí:
Amplitúda vynútených kmitov má tvar:
Rezonancia pre amplitúdu nastane, keď uhlová frekvencia nútiacej sily sa rovná rezonančnej frekvencii danej vzťahom (6.1.7.8).
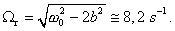
Dosadením rezonančnej frekvencie do výrazu pre amplitúdu, dostaneme rezonančnú amplitúdu:
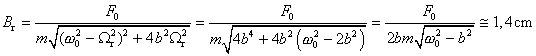
Kontrolné otázky
-
Ako sa mení s časom amplitúda tlmeného harmonického pohybu?
-
Ako sa zmení frekvencia tlmeného pohybu v porovnaní s frekvenciou netlmeného pohybu?
-
Aká sila spôsobuje tlmenie pri harmonickom pohybe?
-
Teleso s hmotnosťou m, zavesené na pružine s tuhosťou k1 koná tlmený harmonický pohyb. Odpor prostredia je úmerný rýchlosti FR = – k2 v. Aký je fyzikálny rozmer konštanty k2?
-
Aký fyzikálny rozmer má koeficient tlmenia?
-
Teleso koná tlmený kmitavý pohyb tak, že okamžitá výchylka v ľubovoľnom čase t má tvar
y = 5 [m] exp(–0,25s–1t) sin(0,5 p s–1t) . Akú bude mať teleso rýchlosť v čase t = 0 s? Aká bude amplitúda jeho kmitov po uplynutí doby jedného kmitu? -
Perióda tlmených kmitov je T1 = 2,5 s, koeficient tlmenia b = 0,2 s–1. Po vykonaní koľkých kmitov klesne amplitúda e-krát ? Aký čas pritom uplynie?
-
Perióda tlmených kmitov je T1 = 1,5 s, koeficient tlmenia b = 2 s–1. Vypočítajte logaritmický dekrement útlmu.
-
Logaritmický dekrement útlmu je d = 0,2. Aký je pomer dvoch maximálnych výchyliek (amplitúd) nasledujúcich po sebe na tú istú stranu?
-
Čo je príčinou vynúteného kmitavého pohybu?
-
Aký je rozdiel medzi rezonanciou amplitúdy a rezonanciou energie?
-
Vynútené kmity sú opísané rovnicou:
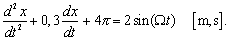
Pri akej uhlovej frekvencii premennej periodickej sily nastane rezonancia?
Príklady
6.2.18 Tenká doštička zavesená na pružine kmitá vo vzduchu s periódou T1. Keď ju ponoríme do kvapaliny s viskozitou h, kmitá s periódou T2. Silu trenia medzi doštičkou a kvapalinou možno vyjadriť Ft = 2 S h v, kde S je plocha doštičky, v jej rýchlosť, h je dynamická viskozita. Vypočítajte dynamickú viskozitu, keď experimentálne určíte T1, T2, hmotnosť doštičky a jej povrch.
6.2.19 Logaritmický dekrement tlmeného harmonického pohybu hmotného bodu je d = 0,07. Určte, za aký čas bude mechanická energia hmotného bodu 12 krát menšia, keď perióda tlmeného pohybu je T = 3s.
6.2.20 Hmotný bod koná tlmený kmitavý pohyb. Za čas t = 50 s hmotný bod stratil 60 % svojej mechanickej energie. Vypočítajte koeficient tlmenia kmitavého pohybu.
6.2.21 Logaritmický dekrement tlmeného harmonického pohybu hmotného bodu je d = 0,03. vypočítajte, koľkokrát sa zmenší amplitúda pohybu po 100 kmitoch.
6.2.22 Aký je logaritmický dekrement tlmeného harmonického pohybu hmotného bodu, keď za 10 s trvania pohybu hmotný bod stratí 50 % svojej mechanickej energie a keď perióda tlmeného pohybu je 2 s?
6.2.23 Pri tlmenom harmonickom pohybe s frekvenciou f = 1 s–1, zmenšila sa amplitúda po desiatich kmitoch na polovičnú hodnotu. Vypočítajte koeficient tlmenia.
6.2.24 Aký je koeficient pružnosti pružín (v počte 4) železničného vozňa, ktorý má spolu s nákladom hmotnosť 50 000 kg, ak pri rýchlosti v = 12 m s–1 sa vozeň začne prudko hojdať vplyvom nárazov na spoje koľajníc? Dĺžka koľajníc je l = 24 m.
6.2.25 Teleso s hmotnosťou m = 0,05 kg koná vynútené kmity na pružine, ktorej konštanta tuhosti je k1 = 10 N m–1, v odporujúcom prostredí, v ktorom sila odporu prostredia je priamo úmerná rýchlosti pohybu s konštantou úmernosti k2 = 0,5 kg s–1 . Vypočítajte rezonančnú frekvenciu.