Zvolíme si takú súradnicovú sústavu, aby os x bola v smere vektora intenzity elektrického poľa E. Bez elektrického poľa je kinetická energia jedného elektrónu daná rýchlosťou tepelného pohybu. t.j.

(a)

a v dôsledku pôsobenia elektrickej sily F = ma = eE sa zväčší zložka rýchlosti v smere osi x na hodnotu

(b)

je čas na prebehnutie strednej voľnej dráhy strednou rýchlosťou. Zložky rýchlosti v smeroch y, z sa nezmenia. Kinetická energia elektrónu je teraz

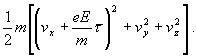(c)

Prírastok energie elektrónu sa rovná rozdielu oboch energií (t.j. „(c) - (a)“)

Ďalej si vezmime jednotku objemu kovu a v nej spočítajme takéto prírastky energie pre všetky elektróny, ktoré sa v tomto objeme nachádzajú. Pri spočítavaní prídeme k tomu, že ich rýchlosti v_x sú rôzne čo do veľkosti a ich orientácie sú v smere aj proti smeru osi x. Pri obrovskom množstve elektrónov bude súčet vektorov v_x rovný nule, t.j. aj v_x = 0. Takže prírastok kinetickej energie elektrónov (ktorých je n v jednotke objemu) bude

Tento prírastok kinetickej energie je za čas . Za jednotku času bude prírastok krát menší, t.j.

Spomenieme si na výraz pre stredný čas (pozri (b)). Ak ho dosadíme do získaného výsledku, vidíme, že zlomok je zhodný s výrazom pre mernú elektrickú vodivosť s (pozri § 4.3). Tento prírastok energie v jednotke objemu za jednotku času je číselne rovný objemovej hustote výkonu p

Keď tento výsledok upravíme pomocou vzťahu pre prúdovú hustotu j = sE a zavedieme vektorové veličiny, dostaneme vzťah , čo je Jouleov zákon v diferenciálnom tvare. Pomocou mikroskopickej elektrónovej teórie sme získali závery, ktoré potvrdzujú experimentálne získané vzťahy (Ohmov zákon, Jouleov zákon).