Pole opísané vektorovou veličinou s nulovou rotáciou sa nazýva nevírové alebo konzervatívne. V takom poli sa zachováva mechanická energia objektu, na ktorý pole pôsobí. Príkladom je elektrostatické pole, ktoré nevykoná žiadnu prácu pri presune elektrického náboja po uzavretej krivke. Z toho tiež vyplýva, že práca, ktorú vykoná elektrická sila (alebo vonkajšia sila) pri presune elektrického náboja z jedného miesta do druhého nezávisí od tvaru trajektórie. To je dôvod, prečo môžeme elektrostatické pole opísať nielen intenzitou elektrostatického poľa E, ale tiež skalárnou veličinou - elektrickým potenciálom j. V elektrostatických úlohách s rovinnou, valcovou alebo guľovou symetriou je výhodné určiť najprv intenzitu elektrostatického poľa E z Gaussovej vety pre elektrický indukčný tok

(10.6.1.1)

potom určiť elektrický potenciál j v ľubovoľnom bode P vzťahom

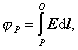(10.6.1.2)

kde O je referenčný bod s nulovým potenciálom. V úlohách bez symetrie určíme najprv elektrický potenciál j integrovaním vzťahu

(10.6.1.3)

kde R je vzdialenosť voľného statického elektrického náboja dq v objeme dV ^/ od miesta, v ktorom potenciál j určujeme. Intenzitu elektrického poľa E potom určíme zo vzťahu

(10.6.1.4)

Pole opísané vektorovou veličinou s nulovou divergenciou sa nazýva nežriedlové alebo solenoidálne. V takom poli sa tok vektora cez ľubovoľný uzavretý povrch rovná nule. Príkladom je magnetické pole opísané magnetickou indukciou B. Tú môžeme určiť v magnetostatických úlohách so symetriou priamo z Ampérovho zákona celkového prúdu (10.4.1.1). Ak úloha nemá symetriu, je výhodné najprv určiť z rozloženia hustoty j elektrického prúdu voľných nábojov magnetický vektorový potenciál A. Magnetická indukcia B bude rotáciou magnetického vektorového potenciálu A. Východiskom k stanoveniu rovnice, ktorá viaže prúdovú hustotu j s vektorovým potenciálom A budú 3. a 4. Maxwellova rovnica pre magnetostatické pole. Z 3. Maxwellovej rovnice (10.5.1.4), divB = 0 vyplýva, že môžeme zaviesť vektorovú veličinu A, ktorá je s magnetickou indukciou B viazaná vzťahom

(10.6.1.5)

Divergencia rotora ľubovoľnej vektorovej veličiny sa totiž vždy rovná nule

lebo vektorový súčin v okrúhlej zátvorke je kolmý k vektorovému „nabla“ operátoru Ñ a skalárny súčin dvoch vektorov na seba kolmých sa rovná nule. Uvažujme o magnetickom poli vo vákuu s materiálovým vzťahom B = m₀H . Násobme 4. Maxwellovu rovnicu rot H = j permeabilitou vákua m₀ a dosaďme vzťah (10.6.1.5). Na ľavej strane novej rovnice získame

kde skalárny súčin dvoch „nabla“ operátorov je Laplaceov operátor D. Pravá strana novej rovnice sa zrejme rovná m₀j, preto má rovnica po úprave tvar

(10.6.1.6)

Zjednodušme poslednú rovnicu voľbou doplnkovej kalibračnej podmienky, ktorá neovplyvní určenie magnetickej indukcie B

(10.6.1.7)

Potom pre magnetický vektorový potenciál A získame vektorovú Poissonovu rovnicu

(10.6.1.8)

Rovnica sa podobá na skalárnu Poissonovu rovnicu pre elektrický potenciál

(10.6.1.9)

preto sa bude riešenie vektorovej Poissonovej rovnice podobať na riešenie skalárnej Poissonovej rovnice. Riešenie skalárnej rovnice (10.6.1.9) je v diferenciálnom tvare dané vzťahom (10.6.1.3). Stačí zameniť j®A, r®j, e®(1/m₀) a v diferenciálnom tvare pre vektorový potenciál A získame

(10.6.1.10)

V integrálnom tvare dostaneme

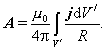(10.6.1.11)

V prípade, že je hustota j elektrického prúdu voľného náboja lokalizovaná v uzavretom vodiči veľmi malého prierezu S ^/ s elektrickým prúdom I, bude zrejme

a po dosadení do (10.6.1.11) dostaneme

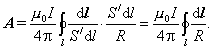(10.6.1.12)

Magnetická indukcia B je rotáciou magnetických vektorových potenciálov (10.6.1.11), (10.6.1.12)

(10.6.1.13)

(10.6.1.14)

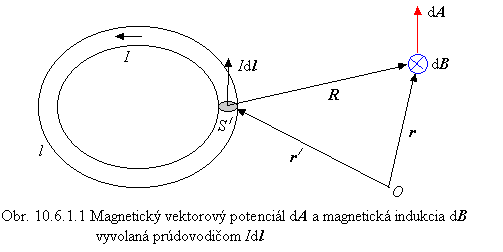
Polohový vektor R = r - r ^/ začína tam kde vektor dl (v objeme dV ^/) a končí v mieste v ktorom určujeme vektorový potenciál A a magnetickú indukciu B, pozri obr. 10.6.1.1. „Nabla“ operátor Ñ pôsobí na nečiarkované súradnice polohového vektora r v skalárnej funkcii 1/R a vytvorí z nej gradient

(10.6.1.15)

Vo vzťahoch (10.6.1.13), (10.6.1.14) sme znamienko „-“ odstránili zámenou poradia vektorov vo vektorových súčinoch.

Vzťah (10.6.1.13) postuloval francúzsky matematik, fyzik a astronóm Pierre Simon Laplace (1749-1827) a nazýva sa všeobecným Laplaceovým zákonom. Vzťah (10.6.1.14) nezávisle od Laplacea formulovali spolu francúzski fyzici Jean Baptiste Biot (1774-1862) a Félix Savart (1791-1841), preto sa nazýva Biotov-Savartov poprípade Laplaceov zákon. Zo vzťahov (10.6.1.11), (10.6.1.12) je zrejmé, že v prípade vybudenia magnetického poľa prúdovou hustotou alebo prúdovodičom ležiacimi v rovine nákresne, vektorový potenciál A v bodoch nákresne nebude mať zložku na nákresňu kolmú. V tomto prípade je magnetická indukcia B v bodoch nákresne na rovinu nákresne kolmá, pozri obr. 10.6.1.1

Biotov-Savartov zákon v diferenciálnom tvare

(10.6.1.16)

umožňuje postulovať vzťah pre určenie magnetickej indukcie B vyvolanej v okolí pohybujúceho sa elektrického náboja. Pretože elektrický prúd I = dq/dt, po dosadení a úprave posledného vzťahu dostaneme

Nahraďme elektrický náboj dq, ktorý vo vodiči prekoná úsek dl za dobu dt bodovým elektrickým nábojom q, ktorý sa vo vákuu pohybuje rýchlosťou v. Potom zrejme v mieste, ktoré má vzhľadom na elektrický náboj polohový vektor R vytvára magnetickú indukciu B

(10.6.1.17)

Zrejme na priamke prechádzajúcej cez elektrický náboj v smere okamžitej rýchlosti sa magnetická indukcia B rovná nule. V prípade viacerých pohybujúcich sa bodových elektrických nábojov sa magnetické indukcie nimi vytvárané vektorovo sčítajú.

Príklad 10.6.1.1

Určte magnetickú indukciu B v strede prúdovej slučky tvaru kružnice polomeru R=10 cm s elektrickým prúdom I=0,5 A! Prúdová slučka sa nachádza vo vákuu.

Riešenie

Magnetická indukcia B v strede prúdovej slučky je kolmá na rovinu slučky a smer určíme pravidlom pravej ruky. Úloha nemá symetriu umožňujúcu použiť Ampérov zákon celkového prúdu, preto použijeme Biotov-Savartov zákon. Pre veľkosť B magnetickej indukcie zo vzťahu (10.6.1.14) vyplýva

Pri úprave sme využili skutočnosť, že vektor R so začiatkom na prúdovej slučke a s koncom v strede prúdovej slučky pri integrovaní nemení veľkosť a neustále zviera s vektorom dl pravý uhol.

Po dosadení zadaných hodnôt dostaneme