 Maxwellova rovnica pre vektor H
Maxwellova rovnica pre vektor H
Maxwellova rovnica spájajúca vektory H a D
V podkapitole o magnetostatike bola odvodená rovnica, vyjadrujúca tzv. zákon prietoku (zákon celkového prúdu) :
![]() (11.2.2.1)
(11.2.2.1)
Tento zákon hovorí, že krivkový integrál vektora intenzity magnetického poľa H po uzavretej krivke sa rovná súčtu všetkých makroskopických prúdov Ik spriahnutých s integračnou krivkou. Pod spriahnutým prúdom rozumieme prúd tečúci takým vodičom, ktorý je s uzavretou integračnou krivkou spojený ako dve susedné ohnivká reťaze.
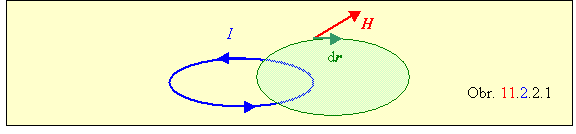
Ľavú stranu rovnice (11.2.2.1) upravíme pomocou Stokesovej vety na plošný integrál. Na obrázku je integračná krivka znázornená zelenou čiarou. Prechod na plošný integrál znamená integrovať po ploche ohraničenej touto krivkou, t.j. po ploche vyznačenej bledozelenou farbou. Aj pravú stranu vyjadríme ako plošný integrál prúdovej hustoty makroskopických prúdov cez tú istú plochu , pričom do vektora prúdovej hustoty j prispievajú všetky spriahnuté makroskopické prúdy:
![]() (11.2.2.2)
(11.2.2.2)
Integračná krivka je ľubovoľná, výsledok nezávisí od jej tvaru. Preto aj integračné medze plošných integrálov v rovnici (11.2.2.2) sú ľubovoľné, takže rovnica bude platiť iba vtedy, keď funkcie za integrálmi na ľavej a pravej strane rovnice budú rovnaké :
![]() (11.2.2.3)
(11.2.2.3)
Táto rovnica je správna iba dovtedy, pokým sa v okolí integračnej krivky nemení vonkajšie elektrické pole. Platí v stacionárnom stave. Maxwell rozšíril pravú stranu rovnice tak, aby platila aj pri zmenách elektrického poľa :
 (11.2.2.4)
(11.2.2.4)
pričom D je vektor elektrickej indukcie. Toto je štvrtá Maxwellova rovnica , ktorá ukazuje, že magnetické pole vzniká nie iba v okolí vodičov elektrického prúdu, ale aj v časovo premennom elektrickom poli.
Pripísanie ďalšieho člena do rovnice vyžaduje podrobné zdôvodnenie. Ak na rovnicu (11.2.2.3) aplikujeme nabla operátor skalárne (t.j. vykonáme operáciu divergencia), na ľavej strane dostaneme div rot H , čo sa identicky rovná nule. Na pravej strane vznikne pritom člen div j , ktorý sa podľa rovnice kontinuity pre elektrický prúd (x.x.x.x.) rovná nule iba v stacionárnom stave. Podľa rovnice kontinuity platí
![]() (11.2.2.5)
(11.2.2.5)
v ktorej r je objemová hustota voľného elektrického náboja, ktorá vystupuje aj v prvej Maxwellovej rovnici divD = r . Túto Maxwellovu rovnicu dosadíme do rovnice kontinuity :
![]()
Preto vo všeobecnosti, aj pri nestacionárnych javoch, platí :
![]() (11.2.2.5)
(11.2.2.5)
Takáto úprava naznačuje, že zatiaľ čo v stacionárnom stave (keď ¶D/¶t = 0) platí div j = 0 , v časovo premenných poliach platí všeobecnejší vzťah div (j + ¶D/¶t) = 0 . Preto pripísanie ďalšieho člena do rovnice (11.2.2.3) znamená jej rozšírenie aj na nestacionárne procesy. Člen ¶D/¶t má rovnaký rozmer ako prúdová hustota, t.j. meria sa v jednotkách A.m-2 . Je to plošná hustota Maxwellovho (posuvného) prúdu, ktorý je jej plošným integrálom.
Fyzikálny význam Maxwellovho posuvného prúdu možno vysvetliť na nasledujúcom príklade. Vodičom nech priteká prúd na platňu kondenzátora, ktorá sa pritom nabíja voľným elektrickým nábojom, čo znamená, že v jej okolí sa mení elektrické pole. Elektrické pole môžeme charakterizovať vektorom elektrickej indukcie D . Pritekajúci elektrický prúd vytvára
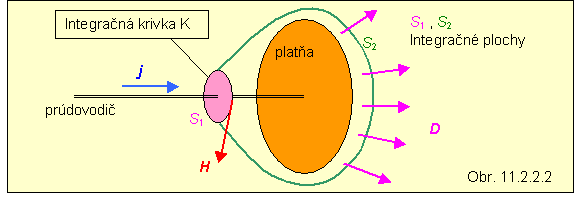
vo svojom okolí magnetické pole, ktoré opisujeme vektorom intenzity magnetického poľa H . Cirkulácia vektora H , t.j. jeho dráhový integrál pozdĺž integračnej krivky (obr.) sa rovná pritekajúcemu prúdu, lebo prúd prechádza plochou S1 , ktorá je ohraničená integračnou krivkou. Na ploche S1 existuje časť, na ktorej prúdová hustota pritekajúceho prúdu nie je nulová, preto ani plošný integrál na pravej strane rovnice (11.2.2.2) nebude nulový. Plochu S1 však možno nahradiť plochou S2 , ktorá má tvar banky s otvorom tvoreným integračnou krivkou K. Cez túto plochu pritekajúci prúd neprechádza, preto plošný integrál prúdovej hustoty pritekajúceho prúdu cez túto plochu sa rovná nule. Ak by v štvrtej Maxwellovej rovnici na pravej strane chýbala hustota posuvného prúdu, vznikol by nesúlad medzi pravou a ľavou stranou rovnice (11.2.2.1) . Prítomnosť posuvného prúdu však kompenzuje tento nedostatok. V miestach, kde sme zvolili plochu S2 , sa počas pritekania elektrického náboja na platňu kondenzátora mení elektrické pole. Derivácia vektora D sa preto nerovná nule a rovnako ani plošný integrál hustoty posuvného prúdu cez plochu S2 . Potom opäť dochádza k rovnosti ľavej a pravej strany rovnice (11.2.2.1) .
Príklad 11.2.2.1 Ukážte, že v platňovom kondenzátore, medzi platňami ktorého je vákuum, možno Maxwellov posuvný prúd I vyjadriť v tvare I = C × (dU / dt ), kde C je kapacita kondenzátora a U napätie medzi jeho platňami.
Riešenie Pre kapacitu platňového kondenzátora platí C = (eoS)/l , kde S je plošný obsah jednej platne, l vzdialenosť platní. Ak na platniach kondenzátora je voľný náboj s plošnou hustotou s, medzi platňami je elektrická indukcia D = s a intenzita elektrického poľa E=s/eo. To využijeme pri nasledujúcej úprave:
![]()
čím sme dostali súčin plošného obsahu platne kondenzátora s hustotou Maxwellovho prúdu. Preto je to Maxwellov prúd.
Kontrolné otázky
- Napíšte štvrtú Maxwellovu rovnicu pre stacionárny stav.
- Napíšte štvrtú Maxwellovu rovnicu platnú aj pre nestacionárny stav.
- Vyjadrite všeobecný obsah štvrtej Maxwellovej rovnice.
- Napíšte rovnicu kontinuity pre elektrický prúd.
- Uveďte súvislosť rovnice kontinuity pre elektrický prúd so štvrtou Maxwellovou rovnicou.
- Uveďte čo je Maxwellov posuvný prúd.
- Aký význam má Maxwellov posuvný prúd pri nestacionárnych javoch ?
- Čomu sa rovná cirkulácia vektora H v stacionárnom elektromagnetickom poli ?
- Čomu sa rovná cirkulácia vektora H v nestacionárnom elektromagnetickom poli ?
