 Rovinná elektromagnetická vlna
Rovinná elektromagnetická vlna
Diferenciálna rovnica vlnenia (11.3.1.4) má rôzne riešenia, ale za najvýznamnejšie považujeme riešenia v tvare rovinnej vlny a v tvare guľovej vlny. Ideálna guľová elektromagnetická vlna je vyžarovaná bodovým zdrojom. Reálny zdroj (napr. malá vysielacia anténa) má však konečné rozmery a priestorom sa z neho šíria vlnoplochy, ktoré guľový tvar nadobúdajú až vo vzdialenosti niekoľkonásobne presahujúcej rozmery antény. V dostatočnej vzdialenosti od zdroja je krivosť týchto vlnoplôch už pomerne malá a v priblížení môžeme ich malé časti považovať za rovinné. Preto aj rovinná vlna je len istou idealizáciou reálneho prípadu. Na opis vlastností elektromagnetického vlnenia je však veľmi výhodná. Súradnicovú sústavu si možno voliť tak, aby napr. os x mala smer šírenia rovinnej vlny. V takom prípade vektory E a B elektromagnetickej vlny budú závisieť iba od dvoch premenných - času t a priestorovej súradnice x . Napríklad pre vektor E harmonickej elektromagnetickej vlny možno potom napísať rovnicu :
E = Eo sin(wt - kx) (11.3.2.1)
kde w je uhlová frekvencia vlny, k = 2p/l uhlové vlnové číslo a l jej vlnová dĺžka. Vektor Eo predstavuje amplitúdu vlny, pričom je na smer šírenia vlny kolmý. To, že je na smer šírenia kolmý, bude teraz predmetom podrobnej analýzy.
Zo zápisu rovinnej vlny (11.3.2.1) je zrejmé, že vektor E nezávisí od priestorových premenných y a z . Táto skutočnosť sa týka všetkých jeho troch súradníc Ex , Ey a Ez (a teda aj zložiek Ex i , Ey j , Ez k ). Preto pre ich parciálne derivácie platí :
![]() (11.3.2.2)
(11.3.2.2)
To využijeme na dôkaz, že Ex nezávisí ani od premennej x . Použijeme pritom prvú Maxwellovu rovnicu (11.2.4.2) :
![]() .
.
Z uvedeného vidno, že súradnica Ex nezávisí od priestorových premenných. Ďalším výpočtom ukážeme, že nezávisí ani od času. Na tento cieľ využijeme štvrtú Maxwellovu rovnicu (11.2.4.5):
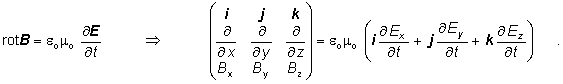
Determinant rozpíšeme, pričom si uvedomíme, že na základe rovníc (11.3.2.2) derivácie podľa premenných y a z sa rovnajú nule. Tak dostaneme rovnicu:
![]()
Na ľavej strane rovnice chýba zložka rovnobežná s jednotkovým vektorom i . Preto aj na pravej strane rovnice musí byť táto zložka nulová. Z toho vyplýva, že parciálna derivácia Ex podľa času sa rovná nule. Preto zložka Exi nezávisí od času. Predtým sme zistili, že nezávisí ani od priestorových premenných. Je to teda konštanta. Keďže hovoríme o vlnách, nie o statických poliach, je korektné považovať túto zložku vektora E rovinnej elektromagnetickej vlny, šíriacej sa v smere osi x za nulovú.
Na základe týchto výsledkov tvrdíme, že vektor E rovinnej elektromagnetickej vlny, vystupujúci v rovnici (11.3.2.1), má len zložky v smere osí y a z, takže je kolmý na smer šírenia vlny.
Analogickým spôsobom by sme mohli získať informáciu aj o vektore B , ktorý je tiež kolmý na smer šírenia rovinnej vlny. Dôležitá je však vzájomná orientácia vektorov E a B v tejto vlne. Informáciu o nej získame, keď využijeme tretiu Maxwellovu rovnicu (11.2.4.4), v ktorej vystupuje rot E . Nech
E = j A sin(wt - wx/c) , (11.3.2.3)
kde A je amplitúda vektora E , c fázová rýchlosť vlny. Rovnicu (11.3.2.3) najprv parciálne derivujme podľa času :
![]()
Teraz vypočítame rotE , pričom si uvedomíme, že derivácie podľa premenných y a z , ktoré predpisuje nabla operátor, sa v rovinnej vlne šíriacej sa v smere osi x rovnajú nule:
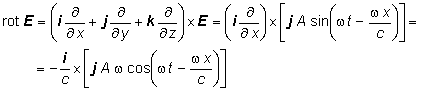
čiže
![]() (11.3.2.4)
(11.3.2.4)
Podľa Maxwellovej rovnice však rot E = - (¶B /¶t) , takže porovnaním s rovnicou (11.3.2.4) získame vzťah medzi vektormi E a B :
![]()
![]() (11.3.2.5)
(11.3.2.5)
Rovnica (11.3.2.5) bude splnená, keď sa splní podmienka

Podľa tohto výsledku vektory B , i a E v rovinnej elektromagnetickej vlne sú navzájom na seba kolmé a v danom poradí tvoria pravotočivú sústavu. Pritom vektor i ukazuje smer šírenia vlny.
Ak si vektory E a B zachovávajú svoj smer (v danom bode priestoru, ktorým vlna prechádza), t.j. s časom sa ich smer nemení, vlna je lineárne polarizovaná. To je prípad rádiových vĺn, najmä z pásma veľmi krátkych vĺn. Pokiaľ ide o svetelné vlny, v danom bode priestoru môžu tieto vektory meniť smer náhodne, vlna môže byť polarizovaná lineárne, ale aj inak, čo je opísané v optike, v kapitole o polarizácii svetla.
Príklad 11.3.2.1 Dosadením do diferenciálnej rovnice vlnenia si overte, že rovnica (11.3.2.3) je jej riešením.
Riešenie Diferenciálna rovnica obsahuje parciálne derivácie vektora E podľa času a podľa priestorových premenných. V tomto prípade sú derivácie podľa premenných y a z nulové, treba vypočítať len derivácie podľa premenných x a t .
(¶E / ¶t) = j A w cos(w t - w x/c) , (¶2E / ¶t2) = - j A w2 sin(w t - w x/c)
(¶E / ¶x) = - j A (w /c) cos(w t - w x/c) , (¶2E / ¶x2) = - j A (w /c)2 sin(w t - w x/c). Porovnaním získame vzťah (¶2E / ¶x2) = (1/c2) (¶2E / ¶t2) , čo znamená, že rovnica (11.3.2.3) je riešením diferenciálnej rovnice vlnenia.
Príklad 11.3.2.2 Pre súradnice vektora E rovinnej elektromagnetickej vlny platia vzťahy Ex = 0, E y = 0, Ez = 2 cos [p × 1015 (t - x /c)] . Napíšte vzťahy pre súradnice B vektora tejto vlny.
Riešenie Zo zápisu súradníc vektora E vyplýva, že vlna sa šíri rovnobežne s osou x , vektor E osciluje rovnobežne s osou z , preto vlnu možno vyjadriť ako E = k Ez . Medzi vektormi B a E v rovinnej vlne platí vzťah (11.3.2.6): B = (1/c) (i x E) = (1/c) (i x k Ez) = - (1/c) j Ez) . Preto vektor B má len zložku v smere osi y :
Bx = 0 , By = - (1/c) 2 cos [p × 1015 (t - x /c)], Bz = 0.
Príklad 11.3.2.3 Rovinná elektromagnetická vlna má amplitúdu E vektora 2 × 10-4 V/m . Vypočítajte amplitúdu vektora B .
Riešenie Použijeme vzťah (11.3.2.6), z ktorého pre veľkosti vektorov platí B = E / c . Po dosadení do vzorca dostaneme
B = 6,66 . 10-13 T .
Poznámka Z výsledku vyplýva, že magnetická zložka elektromagnetickej vlny je v porovnaní s elektrickou malá, čo vyplýva aj priamo zo vzorca (11..3.2.6), v ktorého menovateli je rýchlosť svetla.
Kontrolné otázky
- Kedy by ste elektromagnetickú vlnu považovali za rovinnú ?
- Prečo v rovinnej vlne, ktorá sa šíri pozdĺž osi x , zložky vektora E nezávisia od priestorových súradníc y a z ?
- Ako sú navzájom orientované vektory E , B a smer šírenia vlny ?
- Ako by ste dokázali, že vektory B a E v rovinnej vlne sú na seba kolmé ?
- Aká je to lineárne polarizovaná vlna ?
