 Operátory a ich vlastnosti
Operátory a ich vlastnosti
Pri odvodzovaní a použití základnej pohybovej rovnici kvantovej mechaniky sa stretneme s pojmami operátor fyzikálnej veličiny ako napríklad operátor hybnosti a Hamiltonov operátor. Nakoľko v kvantovej fyzike pojem „operátor“ je bežným pojmom, ozrejmime si jeho význam a spôsob pracovania s operátormi.
Základné vlastnosti operátorov
Definície:
- Operátorom Ô nazývame predpis Ô f(X) = g(X), podľa ktorého funkciám z oboru definície operátora priraďujú inú funkciu z oboru hodnôt operátora.
Operátory budeme označovať strieškou nad príslušnou veličinou. Vo fyzike nás budú zaujímať operátory určitých fyzikálnych veličín, ktoré budú lineárne operátory. Najčastejšie používané pojmy a vlastnosti operátorov možno zhrnúť:
Nech pre každý operátor  a Y , definovaný na množine D, a pre ľubovolné funkcie y1 , y2 , y ![]() D a pre ľubovolné komplexné číslo K platia vlastnosti:
D a pre ľubovolné komplexné číslo K platia vlastnosti:
1) Â(y1 +y2) = Ây1 + Â y2;
2) Â(ky) =K (Ây),
potom operátor  nazývame lineárnym operátorom .
Súčet dvoch operátorov :
3) (Â + Y ) y = Ây + Y y.
Výsledok je operátor.
Súčin dvoch operátorov:
4) Â Y y = Â(Y )y = Âj , kde Y y = j
predstavuje postupné pôsobenie obidvoch operátorov na danú funkciu. Výsledok je operátor.
5) Â Y ≠ Y Â - súčin dvoch operátorov vo všeobecnosti nie je komutatívny, t.j. záleží od poradia pôsobenia operátorov;
6) Výraz [ Â, Y ] = Â Y - Y Â, (13.4.1.1)
nazývame komutátor operátorov ![]() a Y , ktorý je tiež operátorom.
a Y , ktorý je tiež operátorom.
7) Jednotkový operátor Î (operátor identity)
Operátor Î nazývame jednotkovým operátorom, ak pre ľubovolnú funkciu y (x) platí
Îy (x) = y (x)
Množina operátorov na Hilberovom priestore stavov tvorí algebru s jednotkovým prvkom.
Hilbertov priestor je množina regulárnych funkcií, t.j. funkcií ktoré sú spojité, jednoznačné, kvadraticky integrovateľné ( existuje integrál zo súčinu komplexnej a k nej komplexne združenej funkcie).
8) Inverzný operátor Â-1 k operátoru  - Â-1 je inverzný operátor ak platí
 Â-1 = Â-1 Â= Î ;
keď j = Ây , y = Â-1j
9) Hermitovsky združený operátor - operátor Â+ sa nazýva hermitovsky združený operátor k operátoru  ak platí
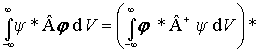
 je hermitovský, ak  = Â+
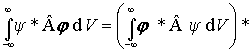 .
.
Axióma: Každej pozorovateľnej fyzikálnej veličine možno priradiť lineárny hermitovský operátor ![]() . K času doteraz nepoznáme operátor, čas vystupuje
. K času doteraz nepoznáme operátor, čas vystupuje
v kvantovej fyzike ako parameter.
- Vlastná funkcia a vlastná hodnota operátora Â
Nech pre pôsobenie operátora  na funkciu y(x) platí rovnica
 y(x) = K y(x) , (13.4.1.2)
potom vlnovú funkciu y(x) – nazývame vlastná funkcia operátora  a číslo K – nazývame vlastná hodnota operátora Â;
Operátor  môže mať viacero vlastných funkcií y n(x) a zodpovedajúcich vlastných hodnôt Kn . Množinu vlastných hodnôt operátora nazývame spektrom. Ak platí rovnica:
 y n(x) = Kny n(x) (13.4.1.3)
hovoríme o diskrétnom spektre. Spektrum môže byť i spojité.
Poznámka: Pre operátory platia i ďalšie vlastnosti, s využívaním ktorých sa študent na úrovni bakalára v základnom kurze fyziky nestretne. Preto ich na tomto mieste neuvádzame.
- Stredná hodnota fyzikálnej veličiny A, (resp. označenie <A> ), ktorej je priradený operátor Â, v stave opísanom vlnovou funkciou y(x) , je definovaná
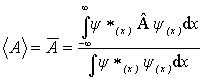 . (13.4.1.4)
. (13.4.1.4)
Pre normové vlnové funkcie, t.j. pre funkcie pre ktoré platí:
![]() ,
,
výraz pre strednú hodnotu fyzikálnej veličiny sa zjednoduší na
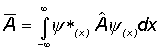 , (13.4.1.5)
, (13.4.1.5)
kde ![]() je komplexne združená funkcia k y1.
je komplexne združená funkcia k y1.
Najpoužívanejšie operátory vo fyzike
V tomto paragrafe zhrnieme najviac používané operátory, s ktorými sa stretneme v nasledujúcich častiach:
1.Operátor súradnice x, (resp. y, z)
![]()
2 .Operátor x-ovej zložky hybnosti ![]()
![]() , (13.4.1.6)
, (13.4.1.6)
resp.
![]() ,
,![]()
![]() ,
,
pretože
![]() .
.![]()
Pre trojrozmerný prípad platí
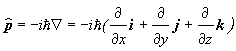 ,
,
kde Ñ je gradient .
3. Hamiltonov operátor
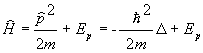 . (13.4.1.7)
. (13.4.1.7)
Hamiltonov operátor je súčtom operátora kinetickej energie a operátora potenciálnej energie Ep. D je Laplaceov operátor D =Ñ·Ñ . (Ñ nabla operátor).
4. Operátor celkovej energie
![]() . (13.4.1.8)
. (13.4.1.8)
5. Operátor z-ovej zložky momentu hybnosti
![]()
8. Operátor štvorca momentu hybnosti
![]()
13.4.1.3 Význam veličiny „komutátor dvoch operátorov“
Komutátor operátorov  a Y nazývame výraz vyjadrený rovnicou (13.4.1.1)
[ Â, Y ] = Â Y - Y Â.
Môžu nastať dva prípady:
· Komutátor dvoch operátorov je rovný nule. Vtedy hovoríme, že operátory komutujú. Fyzikálne veličiny, ktorých operátory navzájom komutujú, sú súčasne merateľné s rovnakou presnosťou, s rovnakou mierou neurčitosti, t.j. nadobúdajú naraz „ostrú hodnotu.“
· Komutátor dvoch operátorov je veličina rôzna od nuly. Vtedy hovoríme, že operátory nekomutujú . Fyzikálne veličiny, ktorých operátory navzájom nekomutujú, nie sú súčasne merateľné s rovnakou presnosťou, ale s istou mierou neurčitosti.
Poznámka: Miera neurčitosti určenia súčinu súradnice x a x-ovej zložky hybnosti px a neurčitosť v určení súčinu energiu a času je daná Heisenbergovými vzťahmi neurčitosti, o ktorých pojednáme v samostatnom paragrafe. Presnejšie určenie jednej veličiny, vedie k nepresnejšiemu určeniu druhej veličiny.
Príklad 13.4.1.1 Nájdite výsledok pôsobenia operátorov (d2/dx2)x2 na funkciu cos x.
Riešenie Pôsobenie operátora na zadanú funkciu možno zapísať
![]()
![]()
Príklad 13.4.1.2 Zistite, či funkcia Y(x) je vlastnou funkciou operátora Â:
a) Y(x) = sin(npx), kde n je celé číslo a Â= d2/dx2
b) ![]()
Riešenie: Na základe definície, danej rovnicou (13.4.1.2), vlnovú funkciu y(x) – nazývame vlastnou funkciou operátora  , ak platí  y(x) = K Y(x), kde K je číslo, ktoré nazývame vlastná hodnota operátora.  . Aplikujme funkciu na daný operátor:
V prípade a):
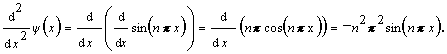
Výslekom je súčin čísla a pôvodnej funkcie. To znamená, že číslo K = –n2p2 je vlastnou hodnotou operátora  a funkcia Y(x) = sin(npx) je vlastnou funkciou operátora Â.
V prípade b):
![]()
Vidíme. že v tomto prípade K= 2ax, kde x je ľubovolná premenná. Musíme skonštatovať, že K nie je číslo a teda funkcia Y(x) nie je vlastnou funkciou operátora Â.
Príklad 13.4.1.3 Zistite či , že operátory ![]() komutujú, a rozhodnite, či x-ová zložka hybnosti a kinetická energia častice je súčasne merateľná s ľubovolnou presnosťou.
komutujú, a rozhodnite, či x-ová zložka hybnosti a kinetická energia častice je súčasne merateľná s ľubovolnou presnosťou.
Riešenie: Napíšeme si jednotlivé operátory a ich komutátor, určený rovnicou
![]() ,
,
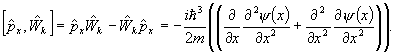
Nech funkcia, na ktorú aplikujeme operátor má tvar Y (x) = 2x3
![]()
Z výsledku vidieť, že komutátory komutujú a teda hybnosť a energiu možno merať súčasne s ľubovoľnou presnosťou.
Príklad 13.4.1.4 Dokážte, že funkcia y(x) = sin kx je vlastnou funkciou operátora  = d2/dx2 a vypočítajte vlastné hodnoty operátora Â. Zistite, ako sa zmenia vlastné funkcie a vlastné hodnoty operátora Â, ak funkcia y(x) spĺňa okrajové podmienky y(0) = 0 , y(l) = 0 .
Riešenie a) Vlastné funkcie sú určené rovnicou (13.4.1.3), podľa ktorej platí:
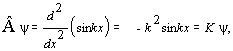
odkiaľ vyplýva , že K = - k2 , kde k je ľubovolné číslo. Takže funkcia y(x) = sin kx je vlastnou funkciou operátora  a –k2 je vlastná hodnota operátora Â
b/ Zistíme, ako sa zmenia vlastné funkcie a vlastné hodnoty operátora Â, ak funkcia y(x) spĺňa okrajové podmienky y(0) = 0 , y(l) = 0 Hraničná podmienka y(0) = 0 je splnená vždy.
y(0) = sin k.0 = sin 0 = 0.
Z druhej podmienky y(l) = 0 dostaneme
y(l) = sin kl = 0 .
Táto rovnosť je však splnená len ak kl = n p pričom n = 1,2,3,...... a pre k musí teda platiť k = n p / l . Uplatnenie okrajových podmienok spôsobí, že vlastnými funkciami operátora  budú iba funkcie
yn(x) = sin kx= sin n p x/l n = 1,2,3,.... .
Vidíme, že operátor  pri uvážení okrajových podmienok, má viac vlastných funkcií a viac vlastných hodnôt. Spektrum jeho vlastných hodnôt bude diskrétne
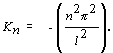 n = 1,2,3, ... .
n = 1,2,3, ... .
Kontrolné otázky
- Vyslovte definíciu operátora fyzikálnej veličiny.
- Uveďte tri príklady operátorov fyzikálnych veličín.
- Je pôsobenie vlnovej funkcie na súčet dvoch lineárnych operátorov asociatívne?
- Je vo všeobecnosti súčin dvoch operátorov komutatívny?
- Napíšte výraz pre komutátor dvoch operátorov fyzikálnych veličín.
- S čím súvisí hodnota komutátora dvoch operátorov fyzikálnych veličín?
- Uveďte príklad dvoch operátorov, ktorých komutátorov je rovný nule. Čo môžeme povedať o týchto fyzikálnych veličinách?
- Uveďte príklad dvoch operátorov, ktorých komutátorov nie je rovný nule. Čo môžeme povedať o týchto fyzikálnych veličinách?
- Definujte pojem vlastná funkcia operátora.
- Definujte pojem vlastná hodnota operátora.
- Môže nadobúdať operátor určitej fyzikálnej veličiny viac vlastných hodnôt?
- Môžeme k operátoru nájsť i viac vlastných funkcií?
- Definujte strednú hodnotu fyzikálnej veličiny
- Napíšte Hamiltonov operátor energie.
